Modellierung, Simulation und Analyse von MEMS-Mikrosensormembranen

Einführung

Die elektrostatische Betätigung, die üblicherweise in MEMS verwendet wird, basiert auf den elektrostatischen Feldern und den Kräften, die sie auf die Strukturen ausüben.
Bei elektromechanischen Aktoren wie HF-Mikroschaltern, Kammantrieben und Drucksensoren ist die durch die elektrostatischen Kräfte verursachte Verformung der Elektroden das Hauptanliegen.

Diese Technologie wurde aufgrund ihres geringen Gewichts, ihrer kompakten Größe, ihres geringen Stromverbrauchs und ihrer Langlebigkeit in vielen Branchen wie der Automobilindustrie und der Biomedizin eingesetzt.

EMS-Simulationssoftware von EMWorks [1]; wurde verwendet, um eine resultierende Auslenkung einer Membran bei angelegter Gleichspannung zu untersuchen; Um dieses Ziel zu erreichen, wurde der elektrostatische Analysetyp mit Kopplung an eine Struktur verwendet.
Bei der durchgeführten Analyse wurde die elektrische Kraft berücksichtigt und die Schwerkraftbeschleunigung ignoriert.

Die Modellgeometrie

Abbildung 1 und Abbildung 2 zeigen die Geometrie des analysierten Modells. Es besteht aus zwei 40 Vierkantmembranen, eine unten und eine bewegliche oben, gesteuert mit zwei Serpentinenfedern.
Die Dicke des Gerätes ist gleich 1 entlang der z-Achse.

Abbildung 1 - Die Geometrie des analysierten Modells

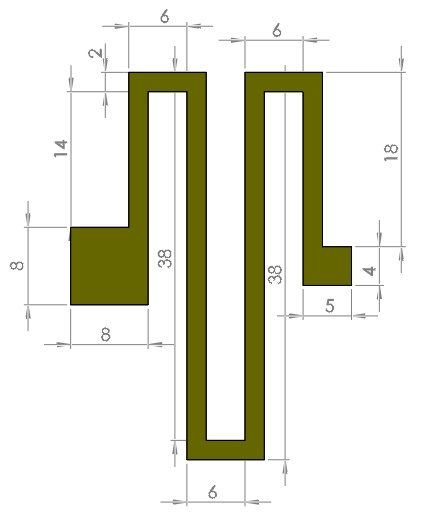
Abbildung 2 - Die Geometrie der Serpentinenfeder

Alle Einheiten sind in Mikrometer angegeben.

Simulations-Setup

Das mit der Strukturanalyse verbundene elektrostatische Modul von EMS wurde verwendet, um die elektrischen Ergebnisse und die mechanische Verformung der sich bewegenden Membran zu berechnen und zu visualisieren.

Um eine Analyse mit EMS durchzuführen, wurden die folgenden wichtigen Schritte ausgeführt:

1. Wählen Sie für alle Festkörper ein geeignetes Material.
2. Definieren Sie die notwendigen elektromagnetischen Eingänge.
3. Übernehmen Sie die strukturellen Randbedingungen.
4. Vernetzen Sie das gesamte Modell und führen Sie den Solver aus.

Materialeigenschaften

Die nachstehende Tabelle 1 fasst die für die Simulation erforderlichen Materialeigenschaften zusammen.

Tabelle 1 - Eigenschaften der dem Modell zugeordneten Materialien

Material Name	Relative Durchlässigkeit	Dichte (kg/ )	Elastizitätsmodul (Pa)	Querkontraktionszahl
Platin	1	2145	170e + 09	0,26
Luft	1	0	Nicht benötigt	Nicht benötigt

Randbedingungen

Elektrische Randbedingung

1. Festspannung 1 (0V)

Die obere Membran ist geerdet, wie in Abbildung 3 gezeigt. Die Pfeile zeigen die Symbole der ihr gegebenen Randbedingung.

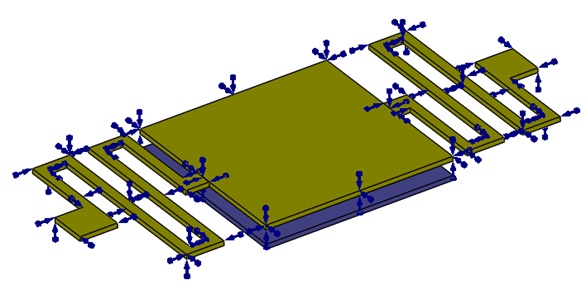
Abbildung 3 - Feste Spannung an der oberen Membran

2. Festspannung 2 (positive Spannung)

Der festen Elektrode ist eine positive Spannung zugeordnet. Abbildung 4 zeigt, wo die Spannung anliegt.

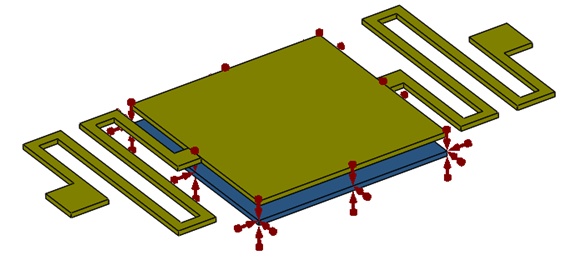
Abbildung 4 - An die untere Membran angelegte feste Spannung

Strukturelle Randbedingung

Feste Randbedingungen gelten für die untere Membran und die Anker der beiden Serpentinenfedern, wie in Abbildung 5 dargestellt:

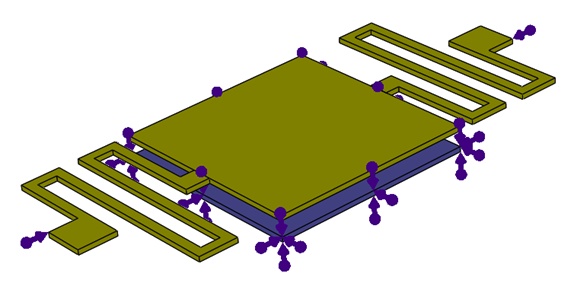
Abbildung 5 - Auf die untere Membran angewendete feste Beschränkung

Ineinander greifen

Die Modellgeometrie enthält keine sehr komplizierten Formen. Auf alle Volumenkörper des Modus wurde ein Mesh-Steuerelement angewendet. Dies würde ausreichen, um genaue elektrische und strukturelle Ergebnisse zu erhalten. Abbildung 6 zeigt das erzeugte Netz.

Abbildung 6 - Das vermaschte Modell

Simulationsergebnisse

An die Bodenmembran wurden unterschiedliche Spannungen angelegt. Die erzeugte elektrostatische Kraft ist der Ursprung der Durchbiegung der oberen Membran.
Die Abbildung 7 zeigt die resultierende Verschiebung als Funktion der von EMS berechneten angelegten Spannung im Vergleich zu den Referenzergebnissen.

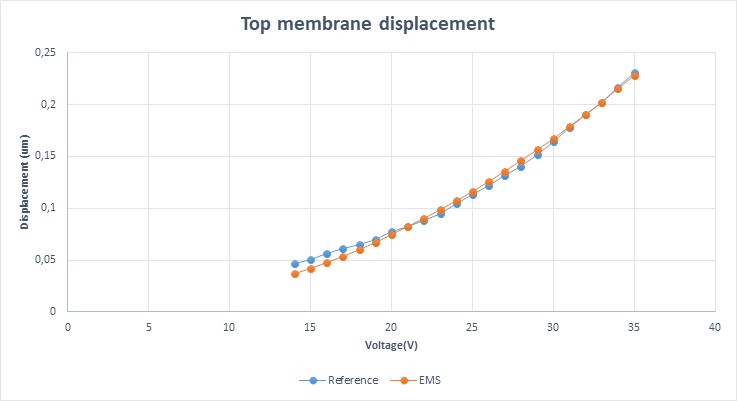
Abbildung 7 - Verschiebung als Funktion der Spannung für EMS und Referenz

Visualisierung der Ergebnisse für 33 V angelegte Spannung:

EMS bietet die Möglichkeit, die resultierende elektrische Starrkörperkraft auf die Strukturteile zu ermitteln. In unserem Fall sind wir daran interessiert, die auf die obere Membran wirkende elektrische Kraft zu ermitteln
Tabelle 2 zeigt die Komponenten des auf die Membran einwirkenden elektrischen Kraftvektors. Die Kraft wird in Newton angegeben.

Elektrische Kraft (Ergebnistabelle)

Tabelle 2 - Die Komponenten des Vektors der elektrischen Kraft

Korrelation zwischen EMS und dem Referenzergebnis:

Tabelle 3 - Vergleich zwischen EMS und den Referenzergebnissen

	EMS Ergebnis	Referenzer
Resultierende Verschiebung unter 3 3V (in )	0,202591	0.201708

Resultierende Verschiebungskurve:

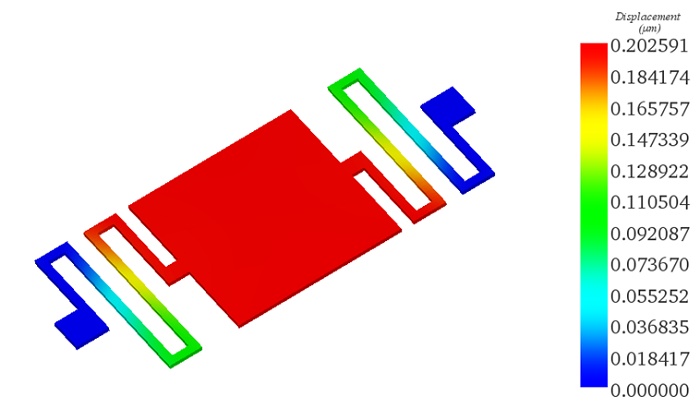
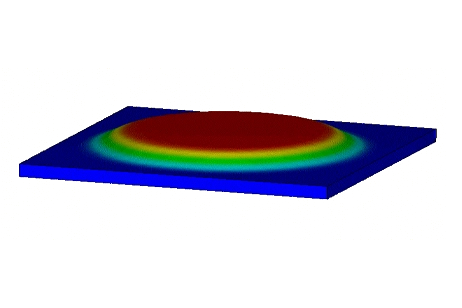
Abbildung 8 zeigt, dass die maximale Verschiebung an der quadratischen Membran auftritt

Fazit

Das strukturelle Verhalten der Mikrosensormembran mit zwei Serpentinenfedern wurde mit Hilfe der EMS-Simulationssoftware untersucht. Die berechnete Verschiebung stimmte gut mit den Referenzergebnissen überein [2].

Diese numerische Analyse half dabei, eine Vorstellung davon zu bekommen, wie das MEMS-Gerät auf verschiedene Gleichspannungseingänge reagiert. im untersuchten Fall nahm die Verschiebung der Bodenmembran mit zunehmender angelegter Spannung weiter zu.

Verweise