Elektrisches Feld im Hohlraum einer geladenen Kugel

Physik

Das Überlagerungsprinzip besagt, dass wenn eine einzelne Anregung in wenige konstitutive Komponenten zerlegt wird, die Gesamtantwort die Summe der Antworten auf einzelne Komponenten ist. Die Anwendung des Prinzips kann anhand des folgenden elektrostatischen Beispiels veranschaulicht werden.
Kugel mit Radius mit einem leeren, kugelförmigen Hohlraum mit einem Radius hat eine positive Volumenladungsdichte Das Zentrum der Höhle ist in der Ferne vom Zentrum der geladenen Kugel (Abbildung 1).

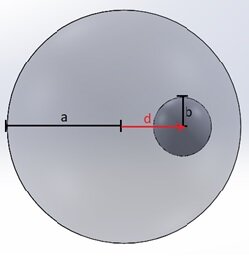
Abbildung 1 - Positiv geladene Kugel mit außermittigem Hohlraum

Nach dem Überlagerungsprinzip kann das Gesamtfeld innerhalb des Hohlraums ermittelt werden, indem einzelne Felder von:

• Ein positiv geladener ( ), gründlich gefüllte Kugel mit einem Radius .
• Eine negativ geladene ( ) Kugel, deren Größe und Position der Kavität entspricht (Abb. 2).

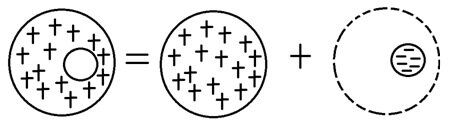
Abbildung 2 - Darstellung eines leeren Volumens durch Überlagerung zweier entgegengesetzter Ladungsdichtedomänen

Das Feld jeder isolierten, gleichmäßig geladenen Kugel in ihrem Inneren in einem Abstand r kann nach dem Gaußschen Gesetz berechnet werden:

Welche Erträge für eine positive Kugel:

Und für eine negative Sphäre:

Wo Vektoren und sind wie in 3 definiert.

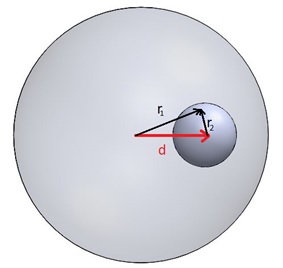
Abbildung 3 - Beziehung zwischen den einzelnen Richtungen des elektrischen Feldes und dem Vektor, der den Hohlraumversatz darstellt

Daher kann das gesamte elektrische Feld im Hohlraum wie folgt berechnet werden:

Aus der letzten Gleichung kann geschlossen werden, dass das elektrische Feld in der Kavität mit einer Richtung konstant ist und dass seine Größe (z und ) ist Die Feldgröße hängt nur vom Wert der Ladungsdichte und dem Abstand ab, um den der Mittelpunkt des Hohlraums vom Mittelpunkt der Kugel versetzt ist.

Modell

Erstellen einer Air Domain

In EMS erfordert die elektromagnetische Analyse die Modellierung der umgebenden Luftregionen, da sich sehr oft ein erheblicher Teil des elektromagnetischen Feldes außerhalb der Teile des simulierten Systems erstreckt. Nachdem das Solidworks-Teil, das die Luftdomäne darstellt, in die Baugruppe importiert wurde, sollten alle Teile davon abgezogen werden. Um dies zu tun:

1. Wählen Sie die Air an dem Solidworks Feature - Manager
2. Klicken Sie auf Komponente bearbeiten auf der Registerkarte Solidworks-Baugruppe
3. Klicken Sie im Solidworks-Menü auf Einfügen/Formen/Hohlraum
4. Wählen Sie im Hohlraum-Feature-Manager Geladene Kugel und Hohlraum als Entwurfskomponenten aus
5. OK klicken .

Abbildung 4 - 3D-Modell einer Kugel mit einem kugelförmigen Hohlraum zusammen mit der umgebenden Luftdomäne

Die Simulation wird als EMS Electrostatic-Studie durchgeführt . Luft wird als Material für alle Teile verwendet.
(Informationen zum Zuweisen von Materialien finden Sie im Beispiel „Berechnen der Kapazität eines Kondensators mit mehreren Materialien“.)

Randbedingungen

Um das elektrische Feld zu simulieren, sollte der großen Kugel eine Ladungsdichtegrenzbedingung und der Fläche der Luftregion eine feste Spannungsgrenzbedingung zugewiesen werden.

So weisen Sie der geladenen Kugel eine Ladungsdichte zu:

1. Klicken Sie in der EMS-Managerbaumstruktur mit der rechten Maustaste auf Laden/Zurückhalten , wählen Sie Ladungsdichte , Dann Volume wählen.
2. Klicken Sie in die Körperauswahl Kästchen und wählen Sie dann die geladene Kugel .
3. Geben Sie auf der Registerkarte Ladedichte 1e-006 ein .
4. OK klicken .

Informationen zum Zuweisen von 0 Volt zu der Fläche der Luftregion finden Sie im Beispiel "Kraft in einem Kondensator".

Ergebnisse

So zeigen Sie die Änderung des elektrischen Feldes entlang der Achse an, die den Mittelpunkt der geladenen Kugel und den Mittelpunkt des Hohlraums verbindet:

1. In der EMS-Krippenstruktur unter Ergebnisse Klicken Sie mit der rechten Maustaste auf den Ordner " Electric Field " und wählen Sie 2D-Zeichnung und dann Linear.
2. Die Eigenschaftsverwaltungsseite für 2D-Elektrofelder wird angezeigt.
3. Wählen Sie auf der Registerkarte Punkte auswählen den Start- und den Endpunkt aus.
4. Geben Sie auf der Registerkarte Anzahl der Punkte 1000 ein.
5. OK klicken .

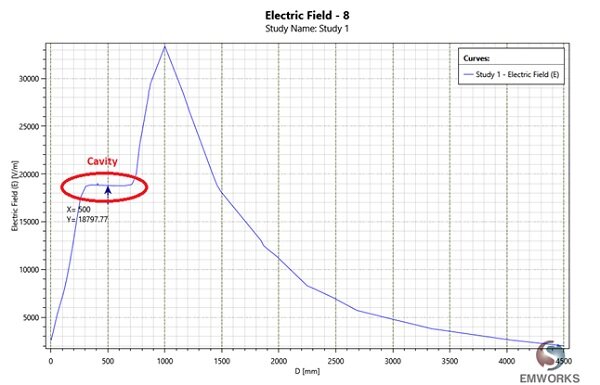
In der erhaltenen Kurve (Abbildung 5) ist klar, dass das elektrische Feld im Hohlraum konstant ist und sein Wert ist , was dem theoretischen Ergebnis sehr nahe kommt. Das Feld in Abbildung 5 nimmt mit dem Radius stetig zu, bis es auf den Hohlraum trifft und bleibt dann unverändert durch den Hohlraum (bis ). Das Feld ragt an der Oberfläche der Kugel empor ( ) und fällt dann mit dem Quadrat des Radius ab.

Verweise

[1] http://jkwiens.com/2007/10/24/answer-electric-field-of-a-nonconducting-sphere-with-a-spherical-cavity/