Analyzing Double-Sided Flat PM Linear Synchronous Motor

Used Tools:

Linear Synchronous Motors

The rising demand for linear motors is mainly due to their advantages over traditional mechanical, hydraulic, or pneumatic systems in manufacturing, as well as their application in high-speed transport and elevators. Linear synchronous motors (LSMs) vary in design, including flat or tubular shapes, single or double-sided configurations, slotted or slotless structures, and iron or air cores, with either transverse or longitudinal flux. This note focuses on analyzing a 3-phase double-sided flat LSM motor prototype using EMWorks2D.

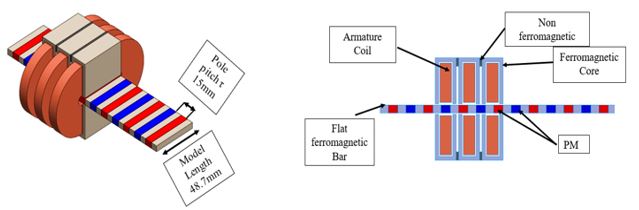
Fig. 1. Flat Slotted Iron Cored Linear Synchronous Motor (FLSM) Model

FLSM Settings

1. Material Selection

The FLSM model utilizes stainless steel 1010 for the core ferromagnetic material and rare-earth sintered NdFeB grade-35 magnets, known for high coercivity and remanence. These materials significantly enhance the motor's performance.

Motor Component	Material
Armature coil	Copper
Flat ferromagnetic bar	Stainless steel 1010
Ferromagnetic core	Stainless steel 1010
Permanent magnet (PM)	N35
Non ferromagnetic core	Aluminum

Table 1. FLSM Material

2. Coercivity Direction and Winding Layout

As shown in Figure 2, the coercivity direction is chosen so that the magnetic flux will be longitudinal from the magnets, the ferromagnetic flat bars will play the role of a magnetic flux conducting material so they will transform the direction of flux to be transversal if a ferromagnetic core is sufficiently close to them.

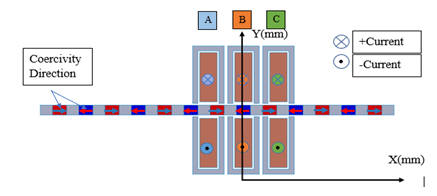
Fig. 2. Coercivity Direction and Winding Layout

3. Defining Distance for Linear Motion

The distance is defined as a mate between the mover (magnets + ferromagnetic bars) and the stationary component, which is in this case the armature (ferromagnetic core + armature winding) as shown in Figure 3.

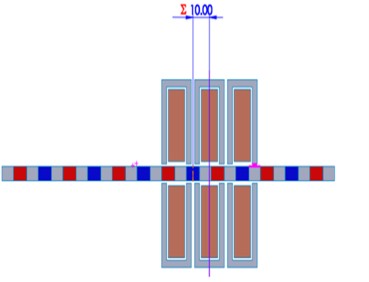
Fig. 3. Distance Definition

Simulation and results

1. Open circuit simulation of FLSM (Detent force and Back EMF)

For an open circuit or no-load simulation in EMWorks2D, set the armature winding to current-driven mode with zero current. The simulation's duration and time step should align to allow the mover to displace by twice the pole pitch, ensuring accurate simulation outcomes.

Parameter	Value
Simulation time	0.03 s
Time step	0.0005 s
Velocity	1 m/s
Distance	30 mm
Initial position	0 mm
Number of turns per phase	280

Table 2. Open Circuit Simulation Settings

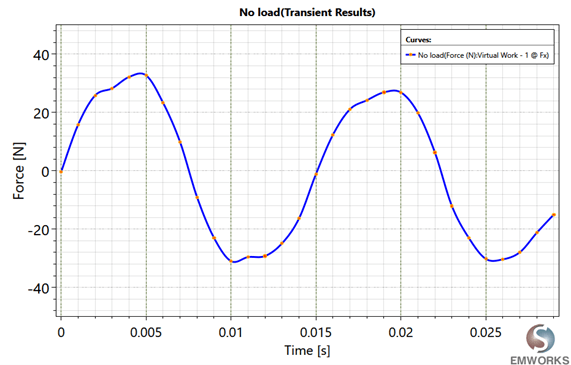
Fig. 4. Detent Force

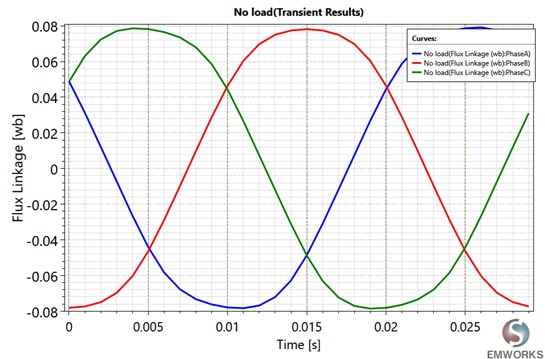
Fig. 5. Flux Linkage

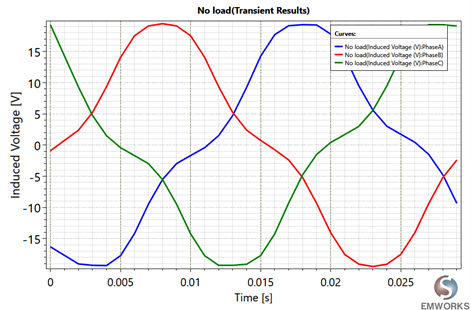
Fig. 6. Induced Voltage

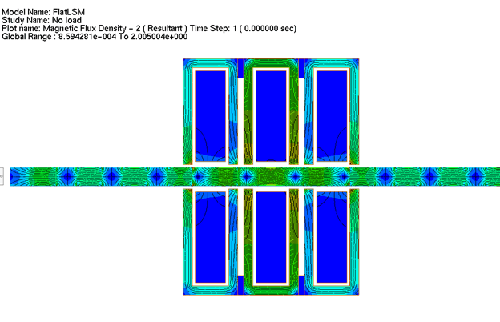
Fig. 7. Flux Density

2. On-load analysis of FLSM (Thrust Values)

During the on-load test in EMWorks2D, armature winding currents vary based on mover position (x). With a moving range equivalent to 15 mm (one pole pitch) and a peak current of 8 A at a linear velocity of 1 m/s, specific current equations for each phase ensure accurate simulation under load.

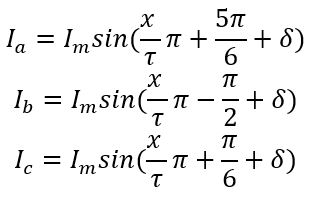
equation 1

Where is the load angle, to get the maximum thrust, different simulations were performed with

Linear velocity depends only on frequency and pole pitch value according to the equation,

Similarly, the values of the current are obtained at a 33Hz frequency.

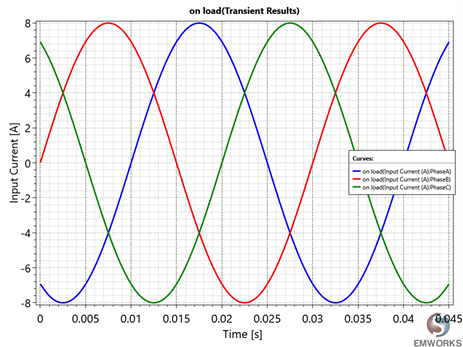
Fig. 8. Input Current Versus Distance

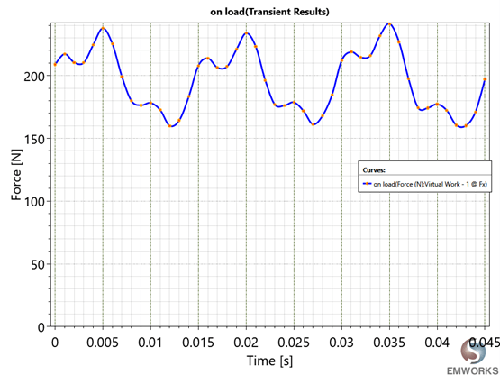
Thrust

Fig. 9. Thrust

The simulation results obtained are tabulated as shown in Table 3.

Parameter	Value
Maximum force, f_max	241.34 N
Minimum force, f_min	160.01 N
Average force, f_av	196.10 N
Force ripple coefficient, k_r	0.414
Maximum detent cogging force	25.66 N

Table 3. Simulation Results

The force ripple coefficient is computed as:

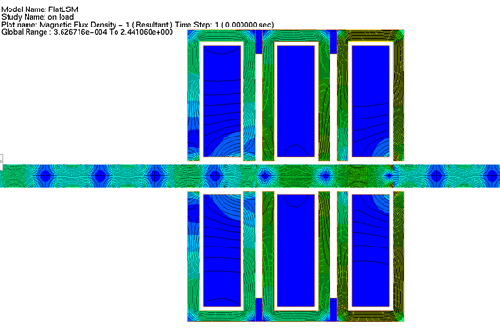
Fig. 10. On- Load Flux Density Plot

3. Dynamic Simulation of FLSM

The FLSM dynamic simulation parameters are shown in Table 4. The armature currents are the same as the on-load simulation and the speed values are computed using the dynamic Newtonian equation

Parameter	Value
Mover mass (kg)	1
Dumping Factor (N-s/m)	0.001
Initial velocity (m/s)	0
Initial position (m)	0

Table 4. FLSM Dynamic Simulation Parameters

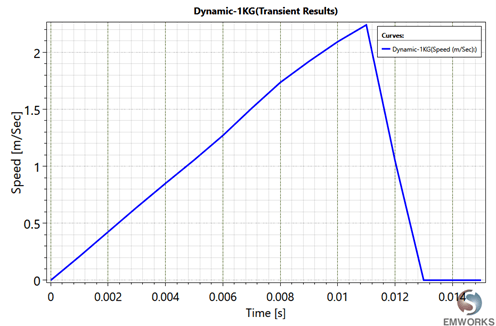
Fig. 11. Dynamic Speed

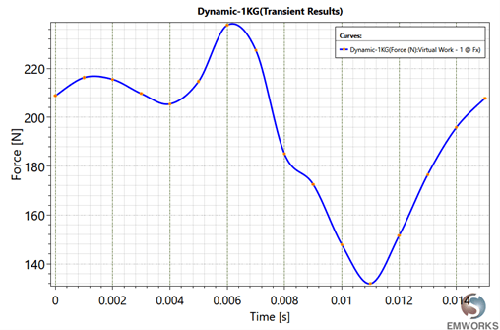
Fig. 12. Dynamic Force

The simulation results obtained are tabulated as shown in Table 5.

Parameter	Value
Maximum force, f_max	237 N
Minimum force, f_min	132 N
Average force, f_av	194.04 N
Force ripple coefficient, k_r	0.5411

Table 5. Simulation Results

Conclusion

In summary, the application note explores the analysis of Flat Slotted Iron Cored Linear Synchronous Motors (FLSM), driven by their increasing adoption across various industries. The focus is on a 3-phase double-sided flat LSM motor prototype using EMWorks2D. Material selection, coercivity direction, winding layout, and defining distance for linear motion are key considerations. Simulation results from open circuit and on-load analyses provide insights into the motor's behavior, while dynamic simulation parameters deepen understanding of its performance dynamics. This comprehensive analysis offers valuable insights for motor design and optimization, showcasing the effectiveness of EMWorks2D simulation.

Reference

[1] Gieras, Jacek F., Zbigniew J. Piech, and Bronislaw Tomczuk. Linear synchronous motors: transportation and automation systems. CRC press, 2016.

Share on