序章
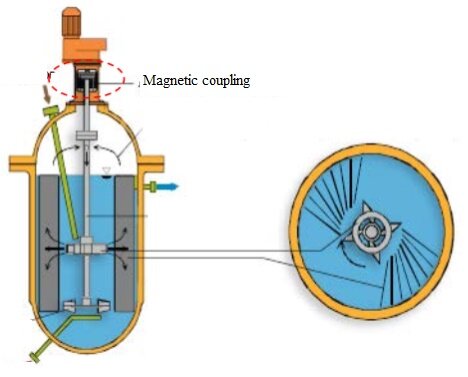
永久磁石結合(またはカプラー) は、機械的接触なしで一次ドライバーから二次フォロワーにトルクを伝達するために使用されます。多くの産業用アプリケーションは、モーターやプロペラ用の外部電気回路を必要としない伝送システムに基づいています。それらは、特に高度なセキュリティ用途や、壁を介した伝送用の密閉された機器で使用されます。
このような結合の機械的構成は、加えられたトルクが定格量を超えると、ねじれにより損傷する可能性があります。したがって、直接の機械的接触がないことで、発生する振動と機械的摩擦損失が減少し、この問題が解決されます。これにより、機械的な従来の結合のメンテナンスと修理の側面を回避でき、システムの寿命を延ばすことができます。この同期結合型は、過負荷に対する本質的な保護を提供する最大伝達トルクを提供します。
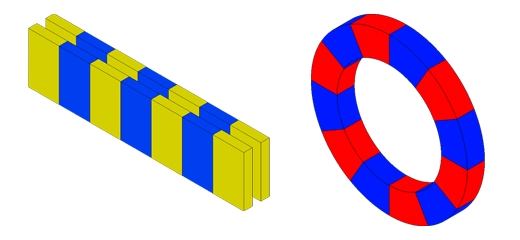
磁気結合は、磁束の方向に応じて、アキシャルまたはラジアル (対面および同軸) の 2 つの異なるトポロジーを持つことができます。それらは両方とも、方向に沿って交互に磁化された永久磁石の円形配列を備えた2つのローターで構成され、同じペアの極数を示します。図 2 は、2 つの異なる永久磁石 (PM) 結合設計を示しています。
特に、軸方向磁束永久磁石 (PM) カップリング トポロジーには、コンパクトな構造という利点があり、より高いトルク伝達を実現できます。それはこの論文で検討され、軸方向に磁化された永久磁石を均等に装備した2つの対向する軟鉄ディスクで構成されています。 PM配置は、南北交互偏波を形成します。両方のローターは、トルク制御係数を定義する適切に調整されたエアギャップの長さによって分離されています。
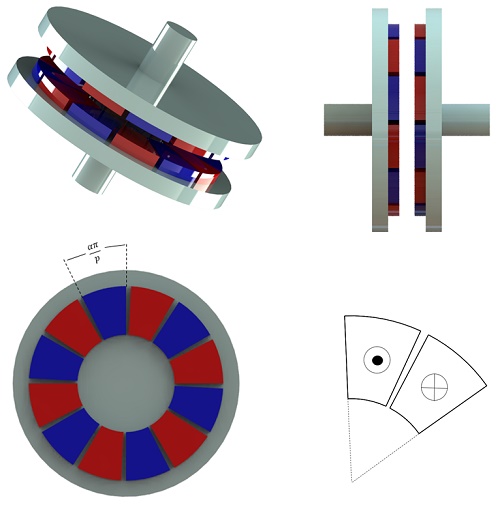
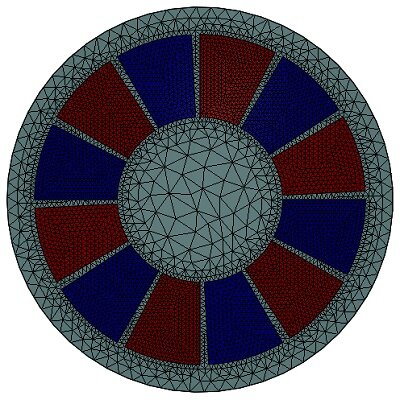
磁気カプラーのトルク特性は、EMS による FEM 3D 電磁界解析を使用して検討し、幾何学的に最適化することができました。これは、PM、極数、空隙距離、および磁気回路の磁気性能に強く関連しています。図 3 は、調査した軸方向磁束 PM カップリング デバイスの詳細な形状を示しています。
![放射状磁束と軸方向磁束の磁気結合のトポロジ [1]](/ckfinder/userfiles/images/Topologies-of-the-Radial-flux-and-Axial-flux-magnetic-coupling.jpg)
問題の説明
静磁モジュールは、EMS のパラメトリック研究を使用して、幾何学的基準に対する磁場分布とトルク挙動を予測するために使用されます。単一の異なるシナリオの実行を通じて、これらの基準のいくつかがカップリングの磁気性能に及ぼす影響を予測することができます。パラメータ化による研究:
- 一定のエア ギャップに対する 2 つのローター間の機械的変位角度 (負荷角度)
- 固定負荷角度に対する平行ローター間のエア ギャップ値。
主な幾何学的寸法は、以下の表 1 に詳述されています。
| 部品 | 寸法 (mm) |
| 外径 | 60 |
| 内半径 | 30 |
| 外部ヨーク半径 | 70 |
| ヨークの厚さ | 10 |
| PMの厚さ | 7 |
| エアギャップの厚さ | 9.5 |
| 極対数 | 6 |
| 磁極ピッチ比に対する磁石の開口部 | 0.9 |
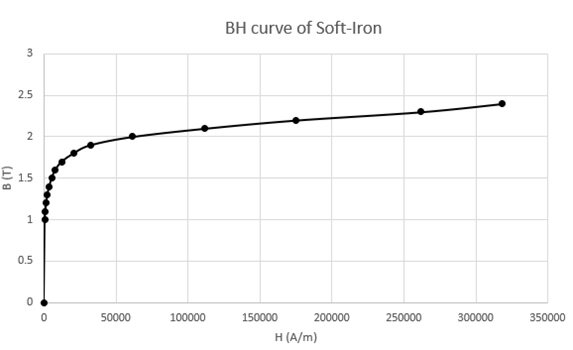
磁石は軸方向に磁化されており、比透磁率は 1 です。強磁性ヨークは、磁気飽和を避けるために厚さ 10mm で選択されており、下図の非線形 BH 曲線によって特徴付けられる軟鉄材料で作られています。
表 2 は、上記の対応する材料特性を定義しています。
| 材料 | 透磁率 | 電気伝導性 | 残存 保磁力 |
| ソフトアイアンヨーク | BH曲線 | 10 | - |
PM-NdFeB | 1 | 0 | 1.25T 994718.4A/m |
パラメトリック スタディ
ケース 1:回転子の同様に磁化された極間の機械的変位角度を変化させることにより: ソルバーは、固定エア ギャップ値 9.5 mm の各シナリオで電磁トルクと静的トルクを計算します。負荷角度15°で最大静トルクが得られます。
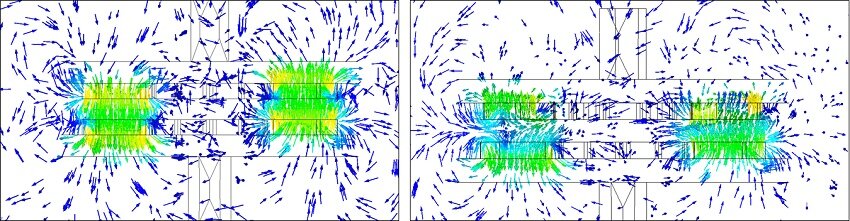
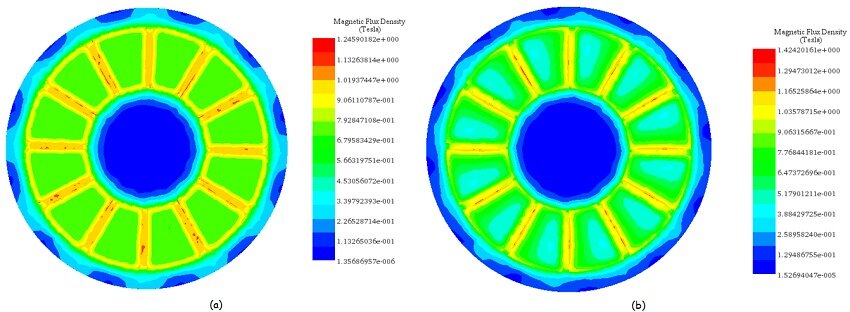
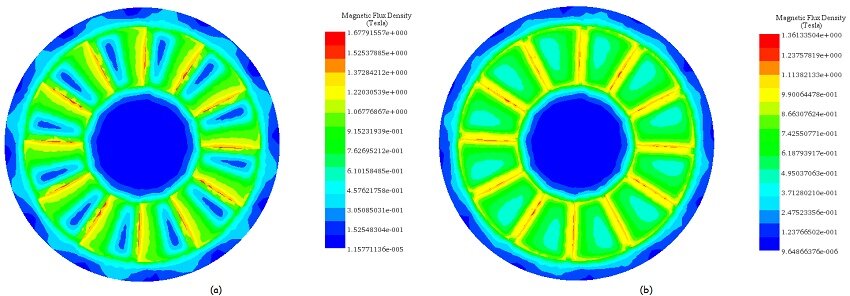
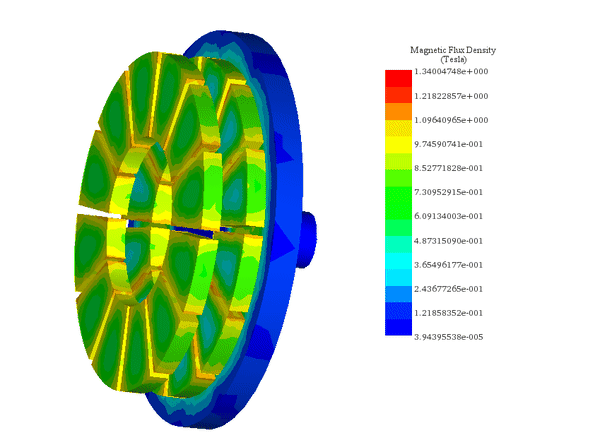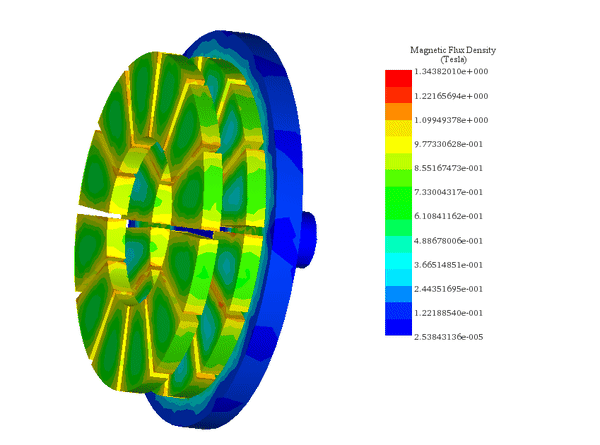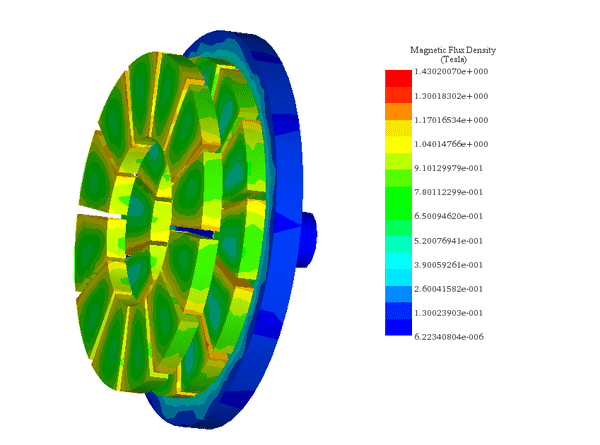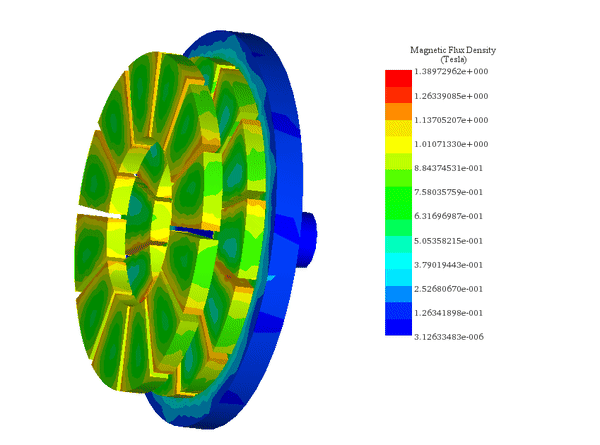
図 6-a) と 6-b) は、カプラの両側の角度ずれがそれぞれ 0° と 15° のときの軸方向磁束密度を示しています。 0° では、同様に分極された極が完全に整列します。磁気抵抗が最小になり、トルクが最小になります。15° では、磁気抵抗はそのピーク値にあります。したがって、磁気トルクはこの位置で最大になります。
次の図は、Ref [3] 内で行われた解析計算と比較して、角度変位に対する計算された静的トルクの EMS の実験結果と FEM シミュレーション結果の間の良好な一致を確認します。角度負荷が 15° を超えると、トルクは次の磁化極との次の位置合わせまで減少します。
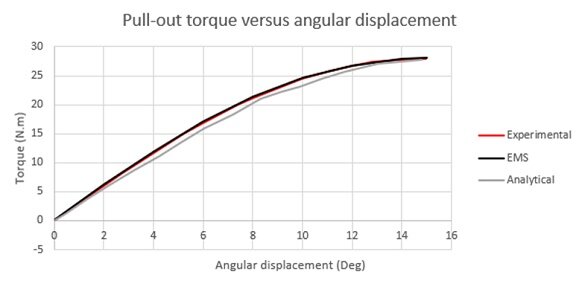
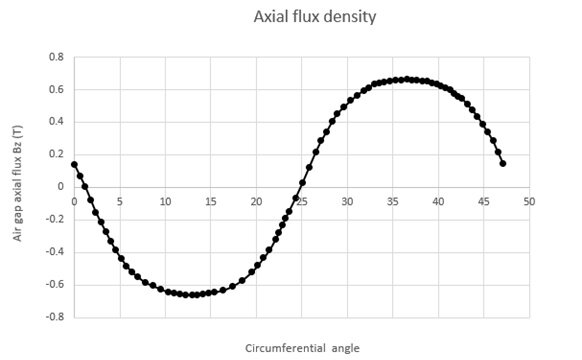
Z 軸に沿った磁束密度分布は、ポールの中心にある中央のエア ギャップ全体で計算され、実験結果と解析結果と比較されます。
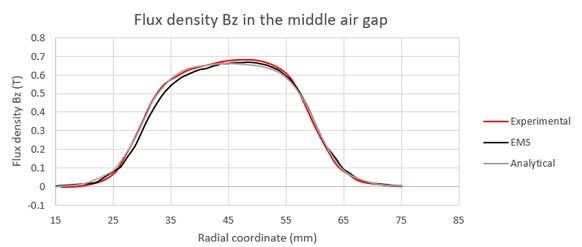
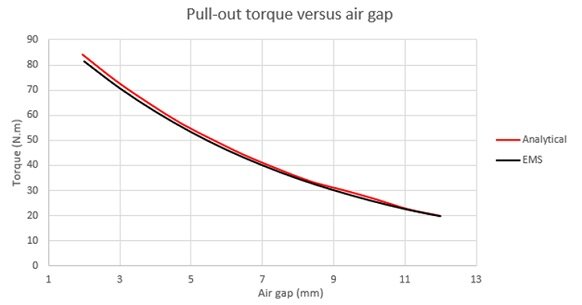
ケース 2: 2 番目のパラメータ化スタディでは、機械的負荷角度を 15° に固定し、エア ギャップ距離の変化により、次の結果が明らかになりました。
検討した磁気カップリングの引き抜きトルクは、磁石間の距離が大きくなるにつれて急速に減少します。エアギャップが 2mm から 7mm になると、最大トルクはほぼ 2 分の 1 になり、このケースでは重要です。
モーションスタディ
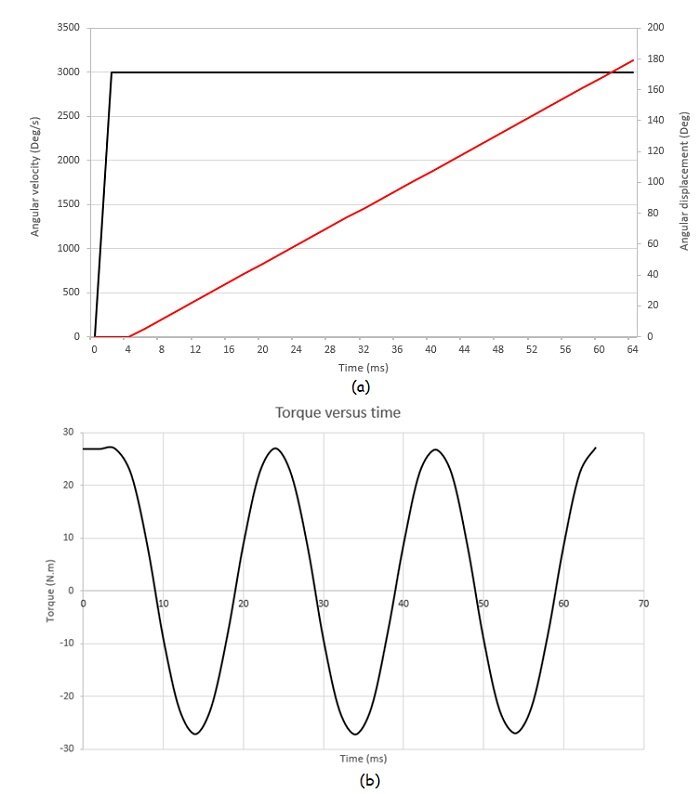
ケース 1: 9.5 mm の固定エア ギャップと 500 rpm (3000 度/秒) の一定の角速度がムーバー ローターに適用され、2 番目のローターが固定されている場合。 SOLIDWORKS のモーション スタディと EMS の静磁スタディを組み合わせることで、時間に対するドライバー ローターの発生トルクと角変位を計算できます。
64 ミリ秒のシミュレーション時間の場合: トルク (Tz) は、互いに分極された極の位置に応じて、達成された最大値と最小値の間で時間に対して振動しています。
ケース 2: 9.5 mm の固定エア ギャップとムーバー ローターに適用される 500 rpm の一定の角速度の場合、次の負荷角度を維持します。 同様に分極された極間: SOLIDWORKS のモーション スタディを EMS の静的磁場スタディと連成させることで、フォロワ ローターの発生トルクと速度対時間を計算できます。
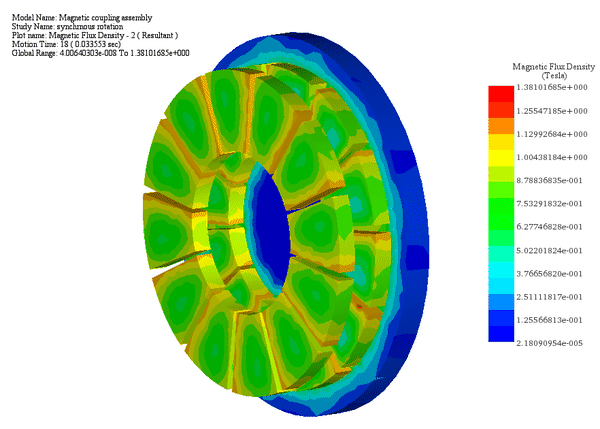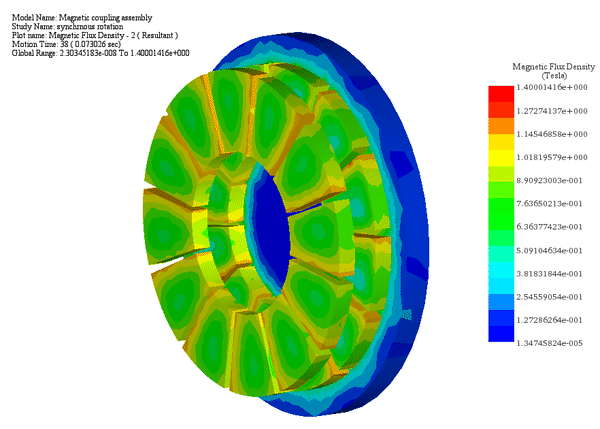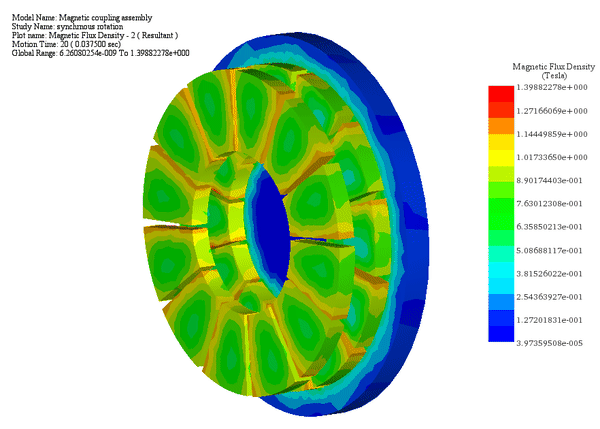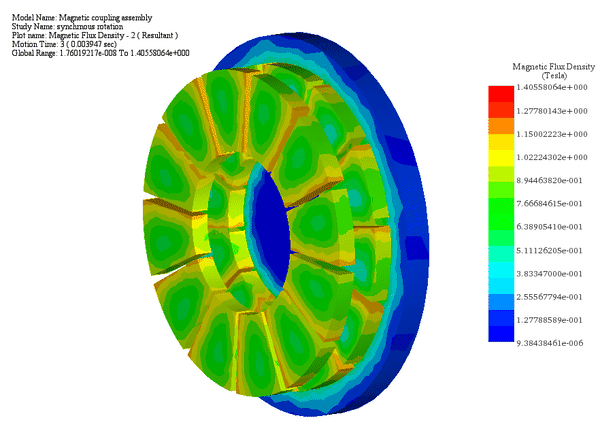
同期機であるため、片側が回転している場合、固定された機械的制約により、片側が同じ速度とトルクで回転し、その間の角度シフトが一定に保たれます。
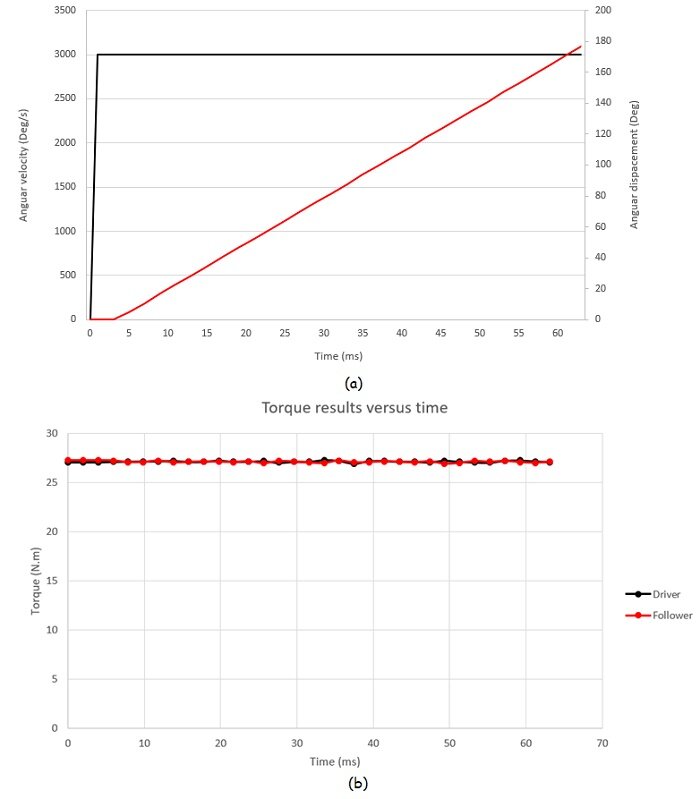
最初の図は、時間に対する各ローターの角速度と変位を示しています。2 番目の図は、約 27 Nm の平均値を持つ動的トルクの結果を示しています。
結論
磁気カプラーでの永久磁石の使用は、回転部品間の機械的接触を必要とせずに 2 つの異なる雰囲気間の分離を必要とするアプリケーションにとって非常に興味深いものです。このような機械装置のトルクと速度の挙動を予測するには、さまざまな幾何学的構成の磁場分布に関する正確な知識が必要です。
EMS のパラメトリック スタディと SOLIDWORKS のモーション解析の使用は、FEM ツールがいくつかの条件下でこのような複雑なシステムを機械的および電磁気的に解析する高い能力を示しています。アキシャルタイプの磁気カップリングの主な利点は、回転するディスク間でトルクを伝達する際の磁場の大きな効果です。
参考文献
[1] Dolisy, Bastien, et al. "A new analytical torque formula for axial field permanent magnets coupling." IEEE Transactions on Energy Conversion 30.3 (2015): 892-899.
[2] Dolisy, Bastien, et al. "Three-dimensional analytical model for an axial-field magnetic coupling." (2014).
[3] Lubin, Thierry, Smail Mezani, and Abderrezak Rezzoug. "Experimental and theoretical analyses of axial magnetic coupling under steady-state and transient operations." IEEE Transactions on Industrial Electronics 61.8 (2013): 4356-4365.