レゾナントワイヤレス給電とは？
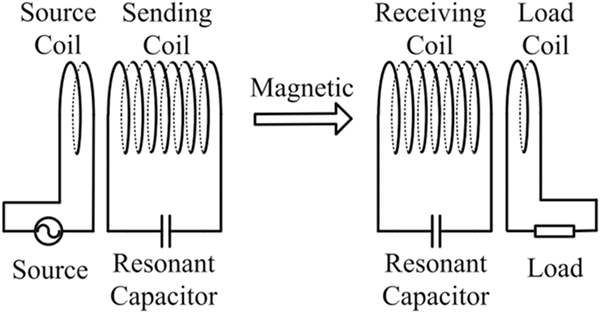
2008 年に MIT の研究者によって導入された共振無線電力伝達(RWPT) は、送信機と受信機の両方に補償コンデンサがあり、共振周波数で動作する無線電力伝達(WPT) です。補償コンデンサは、WPT と比較すると大きな違いがあります。それらはソースから見たインピーダンスの虚数部分を無効にするため、RWPT は WPT と比較してより高い出力電力と効率を実現できます。この優位性は近距離だけでなく、中距離でもコイルサイズに対して発揮されます。当然のことながら、RWPT は近年、電化製品、ウェアラブル ガジェット、携帯電話、電気自動車の充電器 (路上給電を含む) など、無線電力伝送を必要とするさまざまな技術で広く使用されています。
問題の説明
このアプリケーション ノートでは、EMWorks を使用して WPT システム[2]を検討します。このシステムは、2 つの銅プリント コイルで構成されています。図 2 はシミュレートされた無線システムを示し、表 1 はモデルの主な寸法を示しています。後で、共振コンデンサを追加してシステムを WPT から RWPT に変更し、そのような変更から生じるデータを検討します。
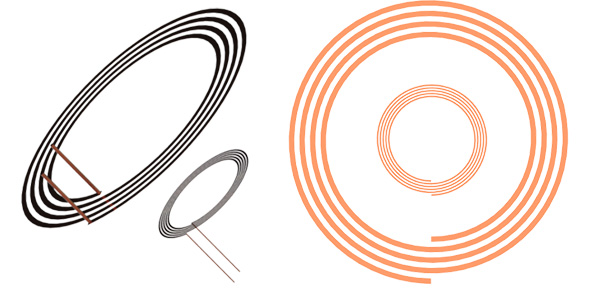
| 外部コイル | 内部コイル | |
|---|---|---|
| 内径 | 27.7mm | 11.64mm |
| 外径 | 41.3mm | 16.14mm |
| トレース間距離 | 1.4mm | 0.3mm |
| トレースの長さ | 1.6mm | 0.5mm |
| トレースの太さ | 40um | 40um |
EMWorks の EMS [3]モジュールを使用して、次の RWPT 問題を調査しました。
R 行列と L 行列を含むシミュレートされた RWPT の回路パラメータ、
結合係数対エアギャップおよびアライメント、
効率対周波数およびジオメトリ構成、
Powersim の結果に対する EMS の結果の比較。
パラメトリック解析
EMS の AC 磁気モジュールを使用して、自己および相互インダクタンス、AC 抵抗、および結合係数を含むコイル パラメータが、異なるエア ギャップ距離および配置に対して計算されます。次に、これらのパラメータを使用して、システムの共振容量と効率を計算します。
表 2 には、エア ギャップ 15 mm の AC インダクタンスと抵抗が含まれています。
| 外部コイル | 内部コイル | |
|---|---|---|
| 自己インダクタンス M (H) | 1.774798e-006 | 1.281031e-006 |
| 相互インダクタンス L1(H) | 1.207742e-007 | 1.207742e-007 |
| 自己抵抗 R (オーム) | 3.410545e-001 | 6.161653e-001 |
| 相互抵抗 Rm(オーム) | 1.920747e-003 | 1.920747e-003 |
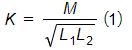で計算されます。 k が大きいほど、エミッタからレシーバ巻線への伝送磁束が高くなります。したがって、効率は結合係数に正比例します[4] 。上記の回路パラメータに加えて、磁場と磁束が計算されます。図 3a) と 3b) は、それぞれ 2 mm と 40 mm のエア ギャップ サイズでの磁束密度の結果の断面プロットを示しています。明らかに、内部コイル、つまり受信機の周囲の磁束は、40mm と比較して 2mm のエアギャップで高くなります。つまり、それぞれ 2 mm と 40 mm で 40 ～ 80 マイクロテスラ対 18 マイクロテスラです。
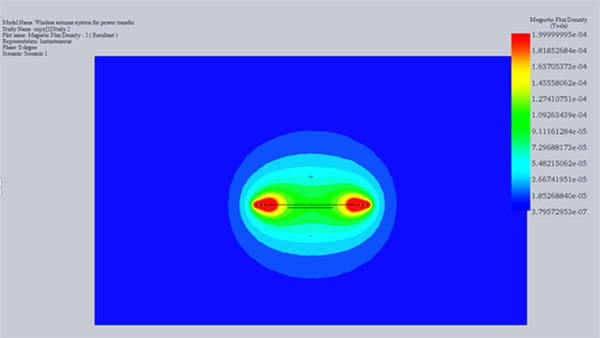
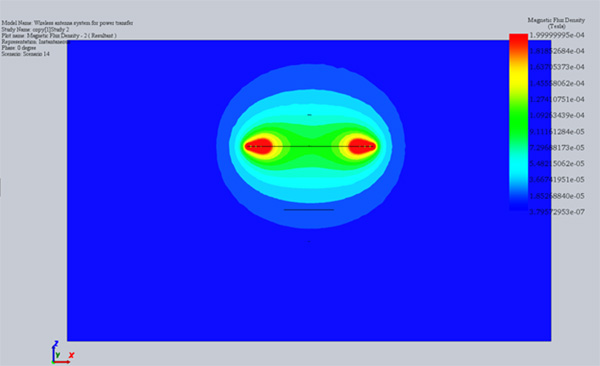
図 3. 磁束の結果、a) エア ギャップ 2 mm、b) エア ギャップ 40 mm
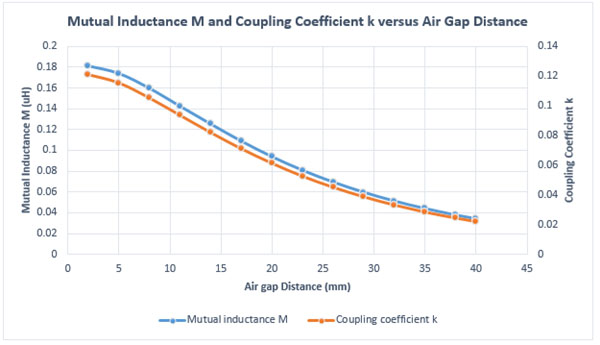
コイル間の距離に対する相互インダクタンス M と結合係数 k のプロットを図 4 に示します。明らかに、M と k はコイル間の距離に反比例します。さらに、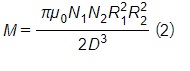
により、相互インダクタンス M の一般的な閉じた形式のソリューションの助けを借りて、反比例は本質的に 3 次です。したがって、良好な結合係数を得るには、コイルをできるだけ近づける必要があります。どれだけ近いか？まあ、それは望ましい結合のレベルに依存します.
図 4. 相互インダクタンス M と結合係数 k の結果とエア ギャップ距離
実際のところ、上記の結論は、図 5 に示すように、開回路動作中の受信機コイルの誘導電圧にも適用できます。
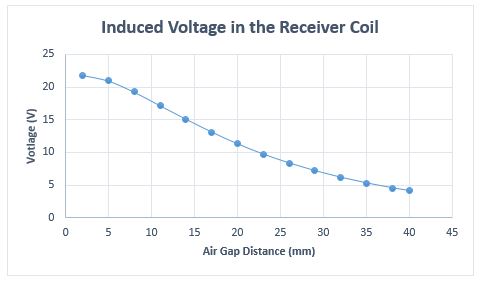
図 5. 受信コイルの誘導電圧とエアギャップ距離
図 6 に示す相互インダクタンス M と結合係数 k の両方の結果は、EMS の別のパラメトリックスタディを使用して、軸方向の位置合わせに対して検討されます。位置ずれが 15 mm を超えると、コイル間の結合が低下します。したがって、検討対象のシステムは、最大 15 mm までの短い範囲のミスアライメントで同じ効率で動作できます。この動作は、受信機のサイズが小さいことに起因する可能性があります。
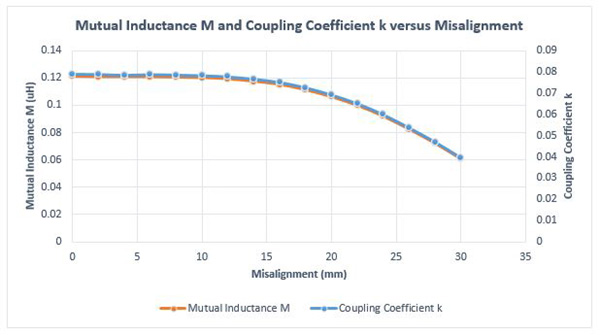
図 6. 相互インダクタンス M とカップリング係数 k の結果とミスアライメント
同様に、図 7 に示すように、位置ずれが 15mm 未満の場合、受信コイルの誘導電圧はほぼ一定であり、その後急激に減少します。
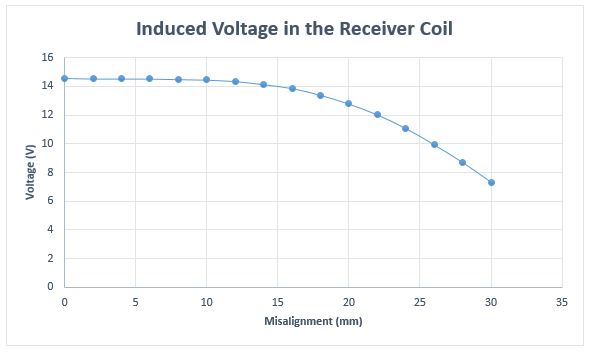
図 7. レシーバ コイルの誘導電圧とミスアライメント
図 8 は、さまざまなミスアライメントに対する磁束密度のアニメーションを示しています。受信コイルに到達する磁束密度は、ある程度のずれまではほぼ一定です。
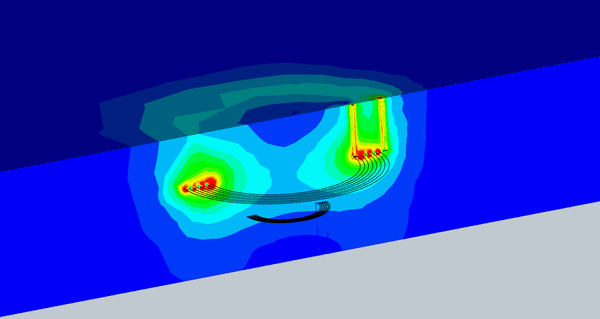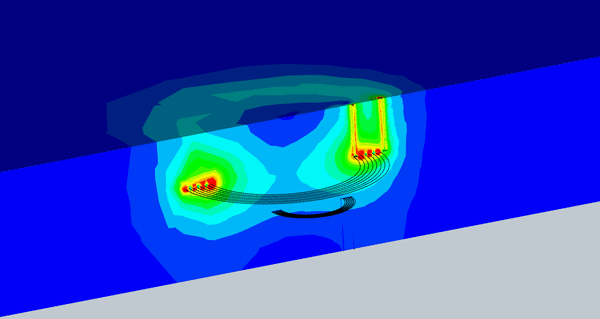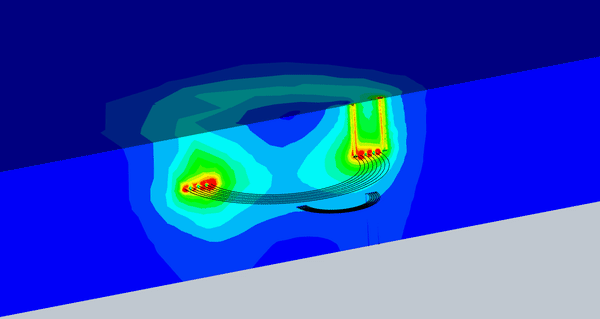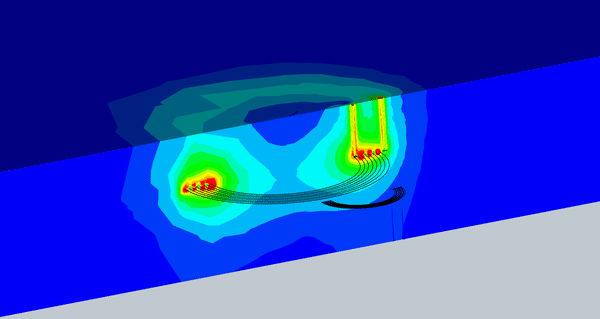
図 8. 磁束とさまざまなミスアライメントのアニメーション
EMS回路結合解析
上で調査した WPT システムでは、結合係数は、エア ギャップが小さく、位置合わせされた状態でも比較的低くなります。 WPT の限界を説明するために、次の式に従って効率を計算します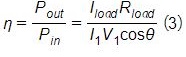
。ここで、V1は入力電圧、I1は一次側の電流、
は電流と電圧の間の位相、Iloadは負荷の電流、Rloadは負荷の抵抗です。
図 9 に示すように、EMS 回路シミュレータを使用して、シミュレートされたシステムの等価回路をモデル化します。巻線 1 と 2 は、WPT システムのコイルです。入力電圧は 2.5 V/13.58 MHz (位相シフトは 0 度) で、負荷は 10 オームの抵抗です。
回路シミュレータに結合された EMS の AC 磁気モジュールを使用して、WPT システムを解決します。送信機と受信機は、15 mm のエア ギャップで整列した位置に維持されます。図 4 に示すように、結合係数はこれらの条件で 0.08 です。
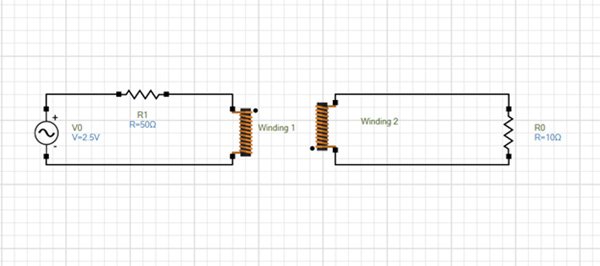
図 9. 調査対象の WPT システムのシミュレーション回路
表 3 は、EMS によって計算された巻線の電流結果を示しています。式 (3) を使用すると、検討したシステムの効率は 0.17% であり、これは確かに低いです。
表 3. EMS によって計算された現在の結果
| EMS によって計算された電流 | |
|---|---|
| 巻線 1 | 4.891836e-003 - j 1.479600e-002 |
| 巻線 2 | -5.844385e-004 + j 1.333585e-003 |
図 10 は、EMS 回路シミュレータを使用してモデル化された新しいシミュレートされた回路を示しています。共振周波数は 13.58MHz で、共振コンデンサはそれぞれ 77.26 pF と 114.42 pF であり、有名な式に基づいて計算されます
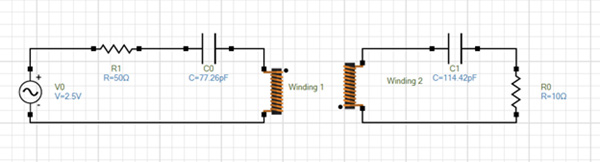
図 10. EMS シミュレータを使用して作成されたシミュレートされた RWPT システムの共振回路
検討対象の RWPT システムの入力電力と出力電力は、周波数に対して計算されます。図 11 に示すように、入力電力と出力電力の両方が共振周波数でピーク値を示します。
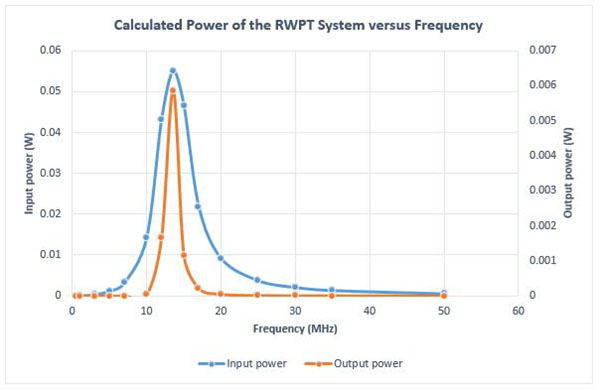
図 11. 入力および出力電力の結果と周波数
図 12 は、さまざまな周波数に対する RWPT システムの効率を示しています。効率は共振周波数で最大になります。共振コンデンサを使用しない場合、効率は約 0.17% ですが、共振コンデンサを使用すると 11% 近くになります。これは、特に結合係数が低いアプリケーションで、共振回路が効率の改善に役立つことを証明しています。
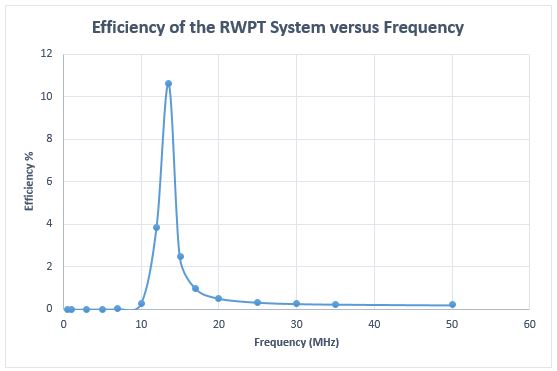
図 12. 効率と周波数
負荷と空隙距離が RWPT システムの効率に与える影響については、次のセクションで調査します。
図 13 に、エア ギャップ距離に対する効率の結果を示します。効率は、エア ギャップ距離が 2 ～ 7 mm の範囲で約 19% の最大値を持ちます。コイル間の距離が大きくなるにつれて低下します。つまり、距離に反比例します。それでも、30mm でも WPT システムよりも効率的です。
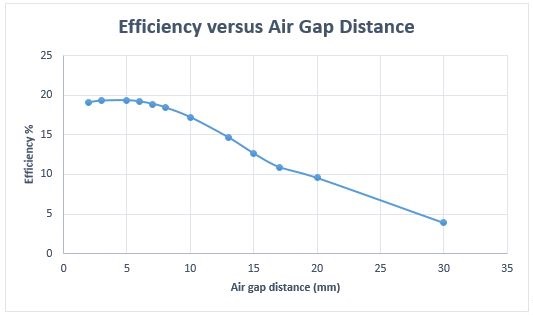
図 13. 効率とエアギャップ距離
図 17 に示すように、負荷を 1 オームから 50 オームまで変化させ、シミュレートされたシステムの効率を EMS によって生成された回路量を使用して計算します。効率は、10 オームの負荷で最大 11% に達するまで上昇します。減少します。したがって、負荷は慎重に選択する必要があります。
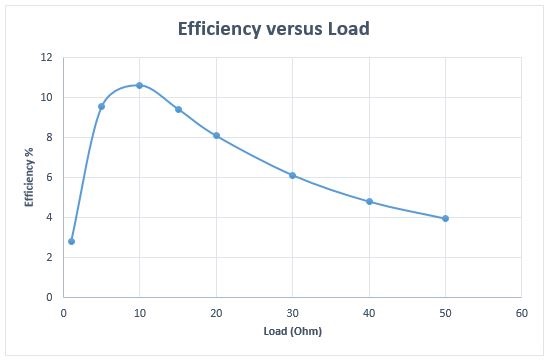
図 14. 効率対負荷
EMS と Powersim [5]の結果の比較
このセクションでは、EMS によって計算された結果を Powersim から取得した結果と比較します。 RWPT 回路は Powersim でモデル化されています。図 15 は、Powersim でのシステムの等価回路を示しています。表 2 に示すように、Powersim で無線コイルをモデル化するために使用される結合インダクタのパラメータは、EMS によって与えられます。
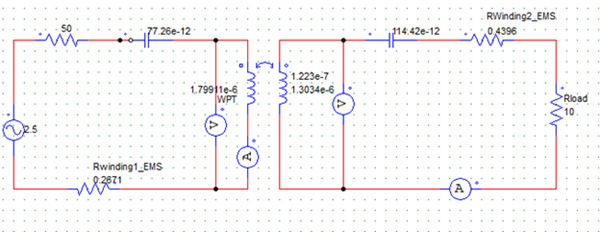
図 15. Powersim の RWPT システムの等価回路
図 16 は、EMS と Powersim によって計算された効率の比較を示しています。明らかに、結果は非常によく一致しています。実際に一致する結果。
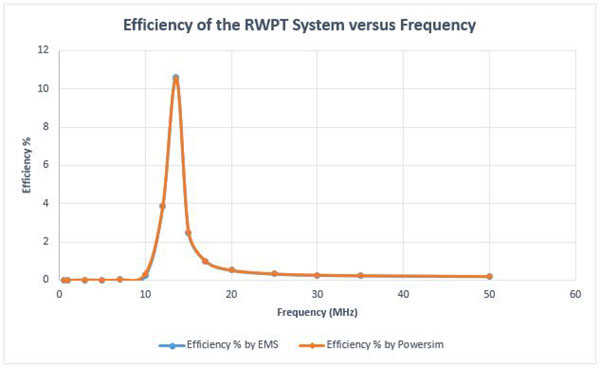
図 16. 効率結果の比較
周波数の関数としてのシステム応答は、Powersim を使用して解析され、結果が図 17 にプロットされます。ボード線図は、振幅出力曲線が共振周波数付近で -16dB の最大値を持つことを示しています。
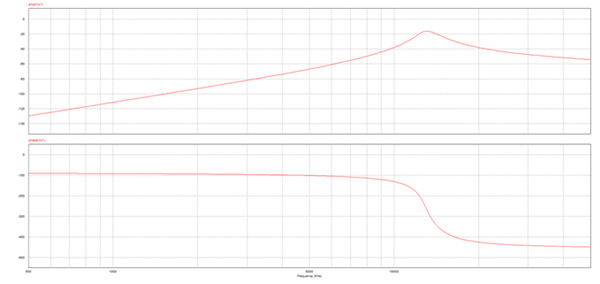
図 17. Powersim から抽出したシステムのボード線図
まとめ
このアプリケーション ノートでは、WPT システムの検討から始めました。コイル間の距離が近い場合でも、WPT は全体的に効率が低いと結論付けました。次に、2 つの共振コンデンサを追加して、WPT を RWPT にしました。実際、RWPT が WPT よりも優れていることを実証しました。それでも、優れた効率を達成するには、負荷を慎重に選択する必要があります。最後の段落では、RWPT システムの EMS の結果を、商用電源ソフトウェア Powersim で得られた結果と比較しました。完全に一致した効率が得られます。
