説明
マイクロストリップラインとストリップラインは、さまざまな電気および電子アプリケーション、特にソリッドステートマイクロ波システムで広く使用されています。ストリップラインは非常に単純な構造をしています。それは一般に、しっかりした導電面にある誘電体基板の上部にある薄い細い金属ストリップで構成されています。
この検証例では、誘電体基板に埋め込まれたストリップ伝送線路を考えます。誘電体基板の比誘電率 εr=12.85。ストリップ導体は、幅 w=5mm の極小の厚さです。ストリップには 1V の電圧が印加されます。基板は、断面の両側から導電性シールドに閉じ込められています。実際、シールド ボックスは接地されており、図 1 に示すように、幅 a=20 mm、高さ b=10 mm です。公表されているデータに対して EMS の結果を検証したいと考えています [1]。
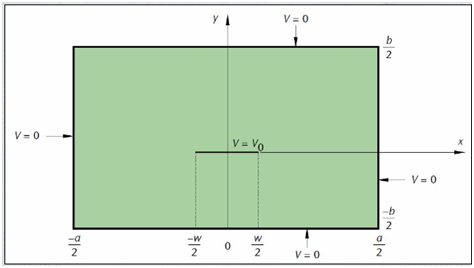
図 1:ストリップ伝送線路の断面
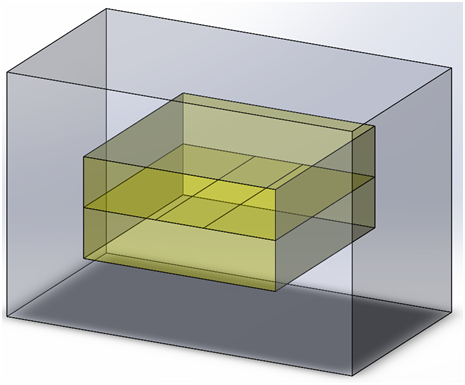
図 2:ストリップラインのソリッド モデル
スタディ
EMS の静電モジュールは、ストリップラインと誘電体基板の電位場を計算するために使用されます。 EMS で静電スタディまたは設計シナリオを作成した後、常に 3 つの重要な手順に従う必要があります。つまり、すべてのソリッド ボディに適切な材料を適用し、必要な境界条件、または EMS のいわゆる負荷/制約を適用し、モデル全体をメッシュ化します。
材料
EMS の静電解析で必要な唯一の材料特性は比誘電率です。これは、誘電体基板と周囲の空気について表 1 に示されています。
| コンポーネント/ボディ | 材料名 | 比誘電率 |
| Air box | 空気 | 1.0 |
| Substrate 4 | TMM-13 | 12.85 |
| Substrate 5 | TMM-13 | 12.85 |
表 1: 2 つの誘電体基板と周囲の空気の比誘電率
材料の適用は簡単です。コンポーネント アイコンを右クリックして、マテリアルを適用するだけです。
負荷/制約
モデルの電気環境と磁気環境を定義するには、負荷と制約が必要です。解析結果は、指定された負荷と制約に直接依存します。負荷と制約は、ジオメトリに完全に関連付けられ、ジオメトリの変更に合わせて自動的に調整されるフィーチャとしてジオメトリ エンティティに適用されます。
このスタディでは、ストリップラインは 1V の電位を持ち、基板の周りのシールドされた導体は接地されています。
メッシング
メッシングは、設計解析において非常に重要なステップです。 EMS は、モデルの体積、表面積、およびその他の幾何学的詳細を考慮して、モデルの全体的な要素サイズを推定します。生成されるメッシュのサイズ (節点と要素の数) は、モデルのジオメトリと寸法、要素サイズ、メッシュ許容値、およびメッシュ コントロールによって異なります。おおよその結果で十分な設計解析の初期段階では、解析を高速化するために、より大きな要素サイズを指定できます。より正確な解を得るには、より小さい要素サイズが必要になる場合があります。
この特定のベンチマークでは、ジオメトリに小さな領域とギャップが伴うため、メッシングはかなり単純です。したがって、グローバル要素サイズは 3 mm に設定され、メッシュ公差は 0.15 mm です。メッシュ要素の総数を増やさずに高い精度を達成するには、大きなフィールドまたは変動が予想される領域にメッシュ コントロールを適用することをお勧めします。 1.2 mm のローカル メッシュ コントロールが誘電体基板に適用されます。図 3 は、結果のメッシュを示しています。

図 3:空気領域のない構造のメッシュ
結果
実行が成功すると、静電モジュールは 4 つの結果フォルダーと結果テーブルを生成します。フォルダーには、電場 E、変位場 D、電位分布 V、力密度がそれぞれ含まれています。結果テーブルにはエネルギーが含まれています。さらに、すべての結果は、フリンジ、ベクトル、等高線、セクション、ライン、およびクリッピング プロットなどのさまざまな形式で視覚化できます。結果は簡単に拡大、エクスポート、分析できます。
この特定のベンチマークでは、電位場の 3D プロットが [1] で報告された結果と比較されます。さらに、EMS のライン プロット機能を使用して、3 点の電位を mm 単位の座標 (10, 3.75)、(11.558, 3.75)、および (12.338, 1.25) と比較します。図 4 ~ 6 が示すように、EMS の結果は [1] の著者によって報告されたものと一致します。
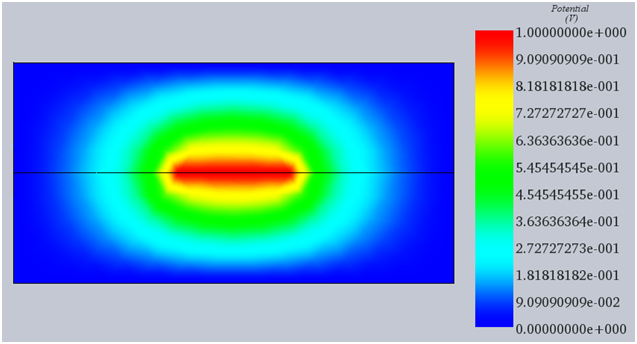
図 4: EMS によって得られた電位場
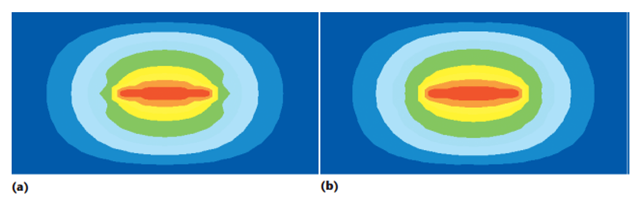
図 5: [1] で報告されている (a) DBEM および (b) FEM を使用した電位場の結果
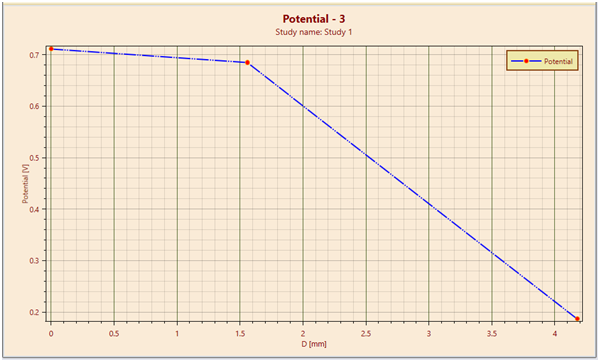
図 6 : EMS で得られた (10, 3.75)、(11.558, 3.75)、(12.338,1.25) 間の電位の折れ線グラフ
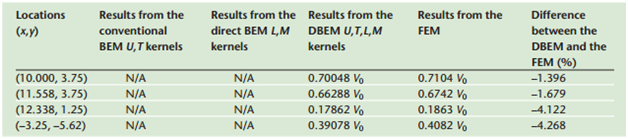
表 2 : [1] で報告されているさまざまな数値手法による電位の結果
3D 電位プロットの結果と基準点、ポイント 1 (0.7112 V)、ポイント 2 (0.6849 V)、およびポイント 3 (0.1867 V) の大きさを、ストリップライン上の最大電位 V0=1 V に対する比率として示します。 [1] から得られた結果と一致します。
結論
このベンチマークは、公開された結果と比較して、EMS の静電モジュールによって達成された高い精度を示しています。
参考文献
[1] Chyuan, S.W.; Liao, Y.S., Chen, J.T.; "An Efficient Method for Solving Electrostatic Problems," Computing in Science and Engineering, Vol. 5, No. 3, May-June 2003, pp. 52-58