Structural Coupling in EMWORKS

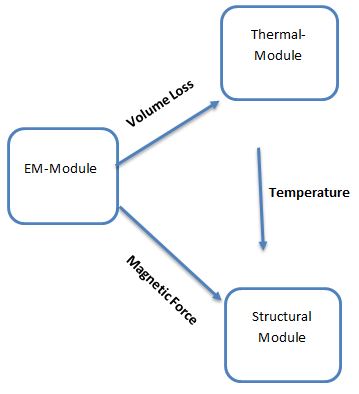
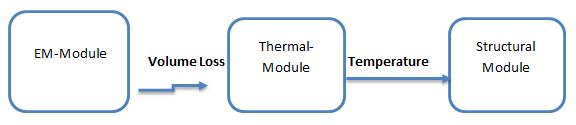
Key Features of EMWORKS Structural Coupling

1. 1

   Electromagnetic → structural load transfer: Map magnetic, electric, or Lorentz forces and pressures from EM analysis onto solid bodies or assemblies.

2. 2

   Static and modal stress analysis: Compute displacement, stress, strain, safety factor, and natural frequencies under electromagnetic loading.

3. 3

   Thermo-mechanical coupling: Use EM losses (J·E, core loss, dielectric loss) as heat sources and evaluate thermally induced deformation and stress.

4. 4

   Multiphysics workflow: Electromagnetic → thermal → structural chaining in one environment for consistent geometry, mesh, and materials.

5. 5

   Material and geometry checks: Compare alternative materials and cross-sections against stress limits, stiffness targets, and fatigue constraints.

Applications for Structural Coupling

• Electric machines (motors, generators)– Magnetic forces on teeth, yokes, and rotors; deformation, vibration, and noise risk.

•  

  Transformers and reactors – Core and winding forces under load, inrush, and short-circuit; clamping stress and tank loading.

• Solenoids and actuators– Plunger/armature forces, contact impact, and housing deformation during operation.

• Busbars, conductors, and rails – Electrodynamic forces under fault currents; mechanical support and bracing requirements.

• Magnetic bearings and levitation systems – Stiffness, deflection, and stress in rotor and stator parts under electromagnetic loads.

• High-power and HV equipment – Structural impact of electromagnetic forces and thermal expansion in switchgear, HV terminals, and clamps.

Results of EMWORKS Structural Coupling

Displacement