物理
円筒状の領域には、均一で時間変化する磁場が含まれています ; B 0は磁場の大きさで、
垂直単位ベクトルです。システムには電荷がないため、変化する磁場が電場
の唯一の原因です.ファラディの方程式によると:
(式1)
またはその場合 z 成分のみを持つ:
(式 2)
ここで、r と円筒座標系の半径座標と角度座標を表します (図 1)。
問題の対称性により、その分析は次のことに注意することで単純化できます。 は
に依存しない、つまり
.したがって、式 2 は次の形式になります。
(式 3)
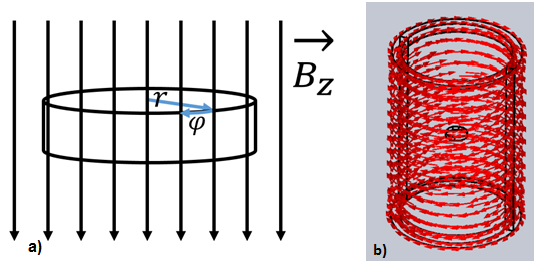
図 1 - a) 垂直磁場内の銅ディスク;b) 変化する磁場は、AC 電流を流すコイルに包まれたシリンダーの内部で生成されます。
につながる
円柱の内部に銅製の円盤を配置すると、誘導電界の結果、渦電流が円盤内に分布します。電流密度
ここで
モデル
銅ディスクの渦電流分布は、 EMSでAC 磁気として簡単にシミュレートできます。![]() 勉強。円筒内に均一な磁場を作成するには、その壁に一定の厚みを持たせて、壁を巻線コイルとして定義できるようにします。内径 15mm、高さ 50mm の円筒を使用して、100 ターンとRMSの巻線コイルを定義する必要があります。 1ターンあたりの電流の大きさ
勉強。円筒内に均一な磁場を作成するには、その壁に一定の厚みを持たせて、壁を巻線コイルとして定義できるようにします。内径 15mm、高さ 50mm の円筒を使用して、100 ターンとRMSの巻線コイルを定義する必要があります。 1ターンあたりの電流の大きさ .Current phase では0º を選択します。これにより、コイルにコサイン電流プロファイルが生成されます。この電流は、比較的均一な大きさの磁束密度を誘導します。
円柱の中心に配置された銅製ディスク (半径: 3mm) のボリューム上。磁場が円柱の内側で垂直方向に整列するようにするには、円柱キャップに垂直磁束境界条件を追加し、円柱壁の内面に接線磁束境界条件を追加します。
境界条件
- EMS マネージャ ツリーで、 Load/Restraintを右クリックします。
 フォルダを開き、 Normal Fluxを選択します
フォルダを開き、 Normal Fluxを選択します .
. - [法線フラックスの面] ボックス内をクリックします。
 次に、[シリンダー キャップ] を選択します。
次に、[シリンダー キャップ] を選択します。 - [OK] をクリックします。
 .
.
- EMS マネージャ ツリーで、 Load/Restraintを右クリックします。
 フォルダを開き、接線フラックスを選択します
フォルダを開き、接線フラックスを選択します .
. - 接線フラックスの面の内側をクリックします
 ボックスから、円柱壁の内面を選択します。
ボックスから、円柱壁の内面を選択します。 - [OK] をクリックします。
 .
.
コイル
渦効果
メッシング
銅ディスクの電流密度の結果を高解像度で取得するには、0.1 mm のメッシュ コントロールを銅ディスクに適用する必要があります。
そうするために、
- EMS マネージャー ツリーで、メッシュを右クリックします。
 フォルダーを開き、 [メッシュ コントロールの適用]を選択します。
フォルダーを開き、 [メッシュ コントロールの適用]を選択します。 .
. - ボディの内側をクリックします
 ボックスから、銅製ディスクの内面を選択します。
ボックスから、銅製ディスクの内面を選択します。 - コントロール パラメータの下で、要素サイズ内をクリックします。
 ボックスに入力し、0.1 mm と入力します。
ボックスに入力し、0.1 mm と入力します。 - [OK] をクリックします。
 .
.
モデルをメッシュ化するには:
- EMS マネージャー ツリーで、メッシュを右クリックします。
 アイコンをクリックし、 [メッシュの作成]を選択します
アイコンをクリックし、 [メッシュの作成]を選択します .
. - [OK] をクリックします。
 .
.
結果
銅ディスクの電流密度分布をプロットするには、電流密度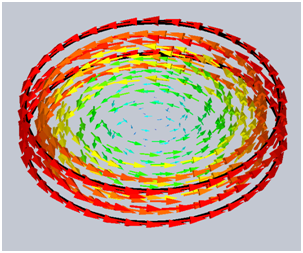
図 2 -銅ディスク内の渦電流密度の 3D ベクトル プロット
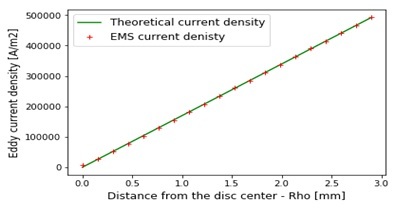
図 3 - EMS と渦電流密度の理論結果の比較