理論
ドメイン内に強力な磁場を発生するため円筒形のコイルを使用されます。円柱に同じワイヤーを何度も巻き付けると、電流による磁場が非常に強くなります。巻き数は円筒コイルのループ数を表します。より多くのループは、より強い磁場をもたらします。
長さ、半径
、巻き数
、電流を運ぶ
の円筒コイルのある時点
で軸で磁場
を決定します。ビオ・サバールの法則によると、電流ループの磁場は次のようになります。
ここは真空透過率です。
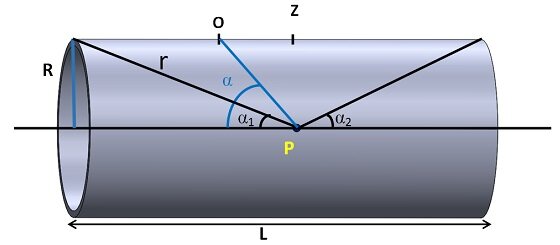
図 1 -円筒形コイルの模式図
円筒コイルの軸上の正味の磁場は、すべてのループの磁場の合計です。円筒の長さを長さの小さな要素 に分割して総磁場を算出できます。
長さ内でコイルの巻数は:
したがって:
長さ内で総電流は:
それぞれの要素及び電流
により、点
で磁場の寄与
は:
長さの要素ごとに円柱の長さに沿った距離
と角度
の値が変わりますが抵抗
の値は一定です。図 1 から、次のことがわかります。
と
式 (2) は次のように微分できます。
結果は次のとおりです。
の式と
の式を (1) に代入できます。
全磁場は、
から
まで積分することにより、軸上の任意の点で算出できます。 :
したがって、この式は、有限長の円筒コイルの軸上の点での磁場を与えます。
モデル
長さ 200mm、半径 5.5 mm、100 ターン、通電電流 10 A の円筒形コイルを Solidworks でモデル化し、EMSの静的磁場解析![]() で解析します。円筒本体には銅が材料として割り当てられ、空気は円筒の内部の空気とアセンブリの残りの部分を覆っています。正確な磁場結果を得るには、十分に大きな空気ドメインを作成する必要があります。EMSで材料を割り当てる方法については、「複数材料コンデンサの静電容量計算」の例を参照してください。EMSで空気領域を定義する方法については、「荷電球の空洞内の電界」の例を参照してください。
で解析します。円筒本体には銅が材料として割り当てられ、空気は円筒の内部の空気とアセンブリの残りの部分を覆っています。正確な磁場結果を得るには、十分に大きな空気ドメインを作成する必要があります。EMSで材料を割り当てる方法については、「複数材料コンデンサの静電容量計算」の例を参照してください。EMSで空気領域を定義する方法については、「荷電球の空洞内の電界」の例を参照してください。
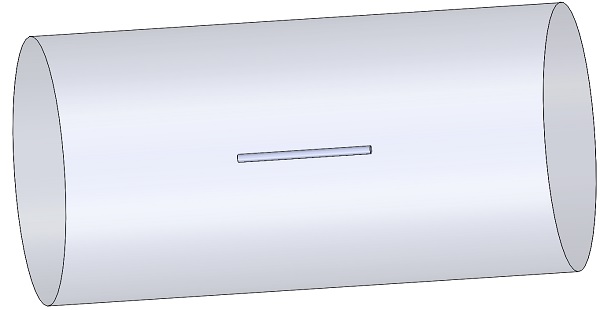
図 2 -検討した例の Solidworks モデル
コイル
円筒形コイルの軸上の磁場を考慮するには、円筒形を使用して巻線コイル![]() を定義する必要があります。このコイルの巻き数
を定義する必要があります。このコイルの巻き数![]() は100で角巻あたり電流の絶対値
は100で角巻あたり電流の絶対値![]() は10Aです。EMSコイルフィーチャーを円筒に適用するには、その断面表面にアクセスする必要があります。したがって、円筒パーツは 2 つのボディに分割する必要があります。その方法については、「電流ループの軸上の磁場」の例を参照してください。図 3 は、コイルの入口ポートと出口ポートを示しています。この場合、出口ポートは入口ポートと同じです。巻線コイルの定義方法については、「磁気回路内の力」の例を参照してください。
は10Aです。EMSコイルフィーチャーを円筒に適用するには、その断面表面にアクセスする必要があります。したがって、円筒パーツは 2 つのボディに分割する必要があります。その方法については、「電流ループの軸上の磁場」の例を参照してください。図 3 は、コイルの入口ポートと出口ポートを示しています。この場合、出口ポートは入口ポートと同じです。巻線コイルの定義方法については、「磁気回路内の力」の例を参照してください。
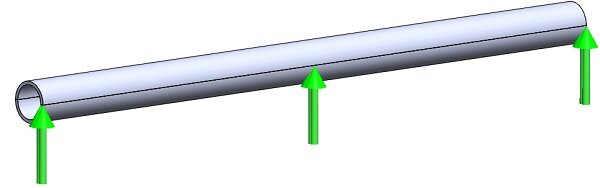
図 3 -コイルの入口ポートと出口ポート
メッシュ生成
EMS解析では、メッシュ生成は非常に重要なステップです。内部空気領域と円柱のメッシュの品質は、正確な磁場計算にとって非常に重要です。メッシュ要素の総数を増やさずに良好な精度を達成するには、要素サイズ![]() 0.75 mm のメッシュ調節を使用します。内部の空気と円筒に適用する必要があります。その方法については、「磁気回路内の力」の例を参照してください。
0.75 mm のメッシュ調節を使用します。内部の空気と円筒に適用する必要があります。その方法については、「磁気回路内の力」の例を参照してください。
結果
円柱の軸に沿った磁場の変化を表示するため解析を実行する前に:
- アセンブリで、ZX 平面を選択し、z軸(コイルの軸)に沿って直線
 をスケッチします、長さはコイルの長さと同じです。
をスケッチします、長さはコイルの長さと同じです。 - 次に、挿入→参照ジオメトリ→点をクリックし、線の両端に参照点を追加します。
- EMSフィーチャーツリーで、スタディ
 を右クリックし、ジオメトリの更新
を右クリックし、ジオメトリの更新 を選択します。
を選択します。 - メッシュ生成してスタディを実行します。
解析が完了したら:
- EMSフィーチャーツリーの結果
 の下で、磁束密度
の下で、磁束密度 フォルダーを右クリックし、2Dプロットを選択してから線形を選択します。
フォルダーを右クリックし、2Dプロットを選択してから線形を選択します。 - 2D 磁束密度プロパティマネージャーページが表示されます。
- 点の選択タブで、インポートをクリックします。
- [OK]
 をクリックします。
をクリックします。
円筒コイルの軸に沿った磁束密度の理論値と EMS の結果を図 4 にプロットします。
EMS の結果がビオ・サバールの法則に準拠していることは明らかです。
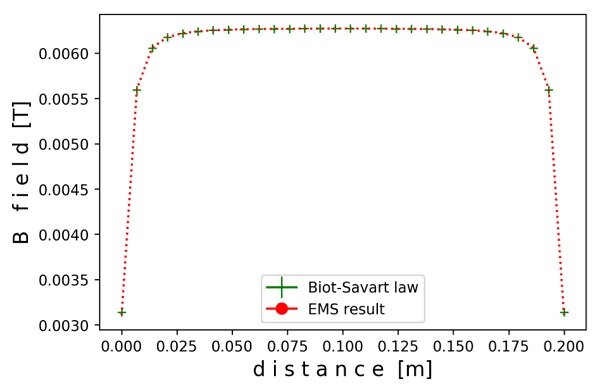
図 4 -円筒コイルの軸に沿った磁束密度の EMS と理論結果の比較