物理
重ね合わせの原理では、単一の励起がいくつかの構成要素に分解される場合、合計応答は個々の要素に対する応答の合計になります。原理の使用は、次の静電気の例で説明できます。 半径の球に
半径の球状空洞があって、正の体積電荷密度
を持っています。空洞の中心は帯電球の中心から
距離にあります（図1）。
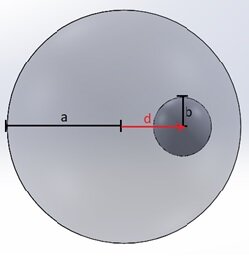
図1-中心から外れた空洞を持つ正に帯電した球
重ね合わせの原理によれば、空洞内の全電界は、以下の個々のフィールドを合計することで見つけることができます。
- 正に帯電した（
）、
半径の完全に詰められた球。
- 負に帯電した（
）、サイズと位置が空洞に一致する球（図2）。
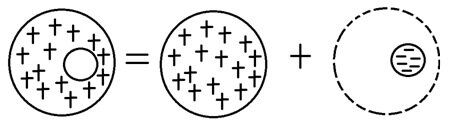
図2-2つの反対の電荷密度ドメインの重ね合わせによる空のボリュームの表現
距離rで内部にある孤立した均一に帯電した球の場は、ガウスの法則から計算できます。
正の球の場合：
負の球の場合：
ここベクトル及び
は図3で定義されているとおりです。
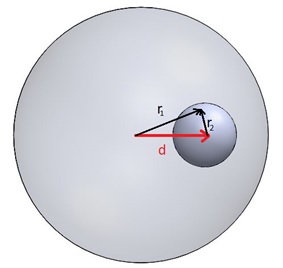
図3-個々の電界方向と空洞オフセットを表すベクトルとの関係
したがって、空洞内の総電界は次のように計算できます。
最後の方程式から、空洞内の電界は方向によって一定であると結論付けることができます。そして
に対して電界の絶対値は
。電界の絶対値は、電荷密度の値と、空洞の中心が球の中心からオフセットされる距離のみに依存します。
モデル
空気ドメインの作成
電磁界のかなりの成分が解析用システムの範囲外に広がることが非常に多いためEMSでは電磁解析で周囲の空気領域のモデリングすることが必要です。空気ドメインを表すSolidworksパーツがアセンブリにインポートされたら、すべてのパーツを空気ドメインから差し引く必要があります。そうするために：
- Solidworks機能マネージャーでAirパーツを選択する。
- Solidworksアセンブリタブでコンポーネントの編集
をクリックする。 - Solidworksメニューで、挿入→金型→キャビティをクリックする。
- キャビティフィーチャマネージャーで、設計コンポーネントとして 荷電球と キャビティを選択する。
- OK
をクリック。
図4-球形の空洞と周囲の空気領域を備えた球の3Dモデル
解析は、EMS 静的電界解析
として実行されます。空気はすべての部品の材料として使用されます。
（材料の割り当て方法については、「複数材料コンデンサの静電容量計算」の例を参照してください）。
境界条件
電界を解析するには、大きな球体に電荷密度境界条件を割り当て、空気領域の面に固定電圧境界条件を割り当てる必要があります。
Charged sphereに電荷密度を割り当てるには：
- EMSマネージャーツリーで、負荷/拘束
を右クリックし、 電荷密度
を選択し、ボリュームを選択する。 - 素子選択
ボックス内をクリックし 、荷電球を選択する。 - 電荷密度タブで、 1e-006と入力する。
- OK
をクリックする。
空気領域の面に0Vを割り当てる方法については、「コンデンサーの強制」の例を参照してください。
結果
帯電球体の中心と空洞の中心を結ぶ軸に沿った電界の変化を表示するには：
- EMSマネージャーツリーで、結果
の下にある、 電界
フォルダーを右クリックし、2D プロットを選択してから、 線形を選択する。 - 2D 電界 Property Managerページが表示されます。
- ポイントの選択タブで、開始ポイントと終了ポイントを選択する。
- ポイントの数 タブで、1000を入力する。
- OK
をクリック。
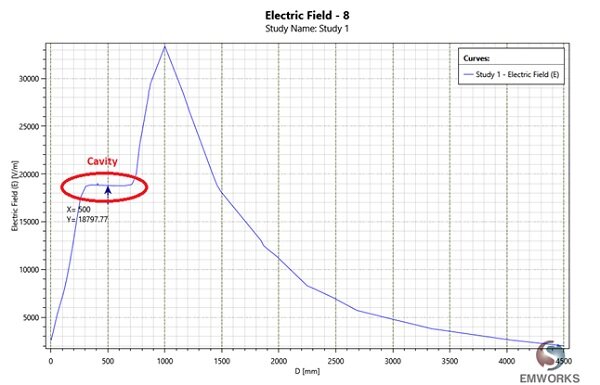
得られた曲線（図5）では、空洞内の電界は一定であり、その値は 、理論上の結果とほぼ一致します。図5の電界は、空洞に達するまで半径とともに着実に増加します。
そしてその後、空洞を通して変わらずに残る（それまで
）。電界は、球の表面でピークに達します（
）その後、半径の2乗で低下します。
参照資料
[1] http://jkwiens.com/2007/10/24/answer-electric-field-of-a-nonconducting-sphere-with-a-spherical-cavity/
