物理
ビオ・サバールの法則により、電流によって生成される磁場を決定することが可能になります。この法則は完全に一般的なものであり、原則として、電流経路の任意の構成に使用できます。
法則は、無限に小さい電流搬送経路磁束密度を生成
距離 r:
ここは真空透過率、
距離方向の単位ベクトル
.対称問題では、解析を単純化し、閉じた形式の解を得ることができます。通電ループの軸上の磁場は、ビオ・サバールの法則を使用して簡単に計算できます。
軸成分
の
ベクトルは、結果として得られる電界強度に寄与します (図 1):
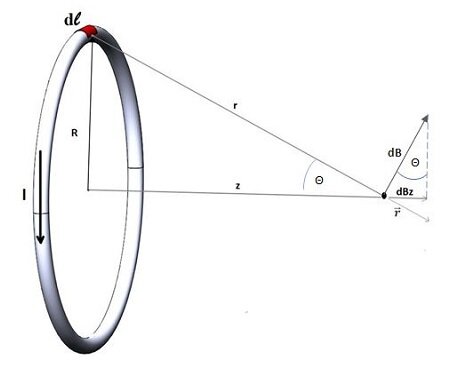
図 1 -電流ループの中心線上のビオ・サバールの法則と場
距離 z の中心線上の点での総磁束密度は、ループの円周にわたって の式を積分することによって求められます。
電流およびループ半径
、軸方向磁場は
.
モデル
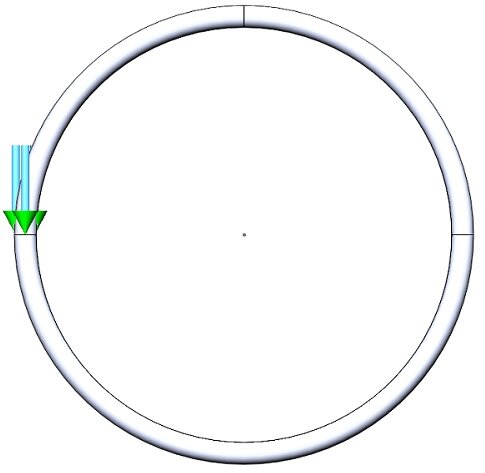
断面積半径 5mm、ループ半径 100mm の薄いトロイドがEMSの静的磁場解析![]() で解析されます。銅はトロイドの材料として規定されていますが、アセンブリの残りの部分は空気で覆われています。正確な磁場結果を得るには、十分に大きな空気ドメインを作成する必要があります。
で解析されます。銅はトロイドの材料として規定されていますが、アセンブリの残りの部分は空気で覆われています。正確な磁場結果を得るには、十分に大きな空気ドメインを作成する必要があります。
EMS で空気領域を定義する方法については、「荷電球の空洞内の電界」の例を参照してください。
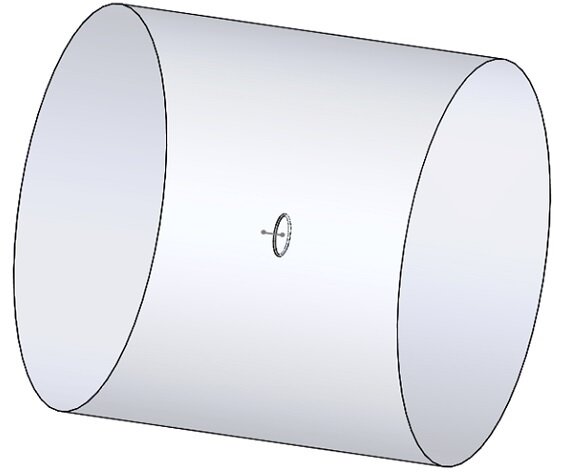
固体コイル
トロイドにEMSのコイルフィーチャを指定するには、断面サーフェスにアクセスする必要があります。したがって、トロイドパーツは 2 つのボディに分割する必要があります。そうするために:
- Solidworks フィーチャー マネージャでトロイドパーツを選択します。
- Solidworks アセンブリ タブでコンポーネントの編集
 をクリックします。
をクリックします。 - Solidworks メニューで 挿入→金型→分割をクリックします
- 分割フィーチャー マネージャで、トリム ツールタブのトロイドの平面図を選択し、パーツのカットをクリックします。
- 結果のボディタブで、 すべて選択をクリックします。
- [OK]
 をクリックします。
をクリックします。
EMSフィーチャーツリーで、コイル![]() フォルダーを右クリックして固体コイル
フォルダーを右クリックして固体コイル![]() を選択します。
を選択します。
コイルのコンポーネント![]() ボックス内をクリックします。
ボックス内をクリックします。
グラフィック領域の左上隅にある (+) 記号をクリックして、コンポーネントツリーを開きます。
トロイドアイコンをクリックします。コンポーネントとソリッド ボディ リストに表示されます。
入力ポート面 ![]() ボックス内をクリックします。次に、入力ポート面を選択します。
ボックス内をクリックします。次に、入力ポート面を選択します。
Exit Port タブで、Same as Entry Portにチェックを入れます。 (図3)
一般的なプロパティ:
- 一般プロパティタブをクリックします。
- デフォルトのコイル タイプを電流駆動コイルのままにします。
- 正味電流
 に100を入力します。
に100を入力します。 - [OK]
 をクリックします。
をクリックします。
結果
トロイドの軸に沿った磁場の変化を表示ため解析を実行する前に:
- アセンブリで、ZX 平面を選択し、直線
 をスケッチしますトロイドの中心から z 軸に沿って進み、長さは 100mm です。
をスケッチしますトロイドの中心から z 軸に沿って進み、長さは 100mm です。 - 次に、挿入→参照ジオメトリ→点をクリックし、線の両端に参照点を追加します。
- EMSフィーチャーツリーで、スタディ
 を右クリックし、 ジオメトリの更新
を右クリックし、 ジオメトリの更新 を選択します。
を選択します。 - メッシュ生成し、スタディを実行します。
解析が完了したら:
- EMSフィーチャーツリーの結果
 の下で、磁束密度
の下で、磁束密度 フォルダーを右クリックし、2Dプロットを選択し、線形を選択します。
フォルダーを右クリックし、2Dプロットを選択し、線形を選択します。 - 2D 磁束密度プロパティマネージャー ページが表示されます。
- 点の選択タブで、始点と終点を選択します。
- [OK]
 をクリックします。
をクリックします。
トロイドの軸に沿った磁束密度の理論値と EMS の結果が図 4 にプロットされています。2 つの解の間の一致は非常に良好です。
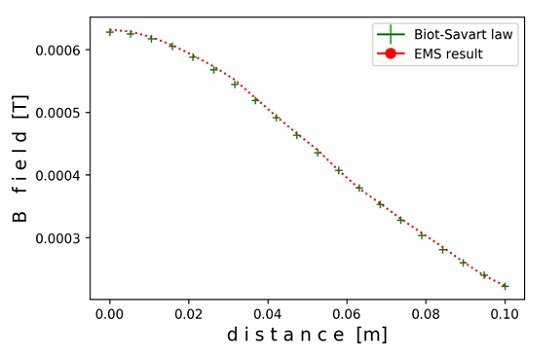
図 4 -トロイドの軸に沿った磁束密度の EMS と理論結果の比較
- EMSフィーチャーツリーで結果
 の下に磁束密度
の下に磁束密度 を右クリック。
を右クリック。 - 3D ベクトル プロット
 およびセクションクリッピング
およびセクションクリッピング を選択します。
を選択します。 - セクション クリッピングタブで、システムの中心線を含むセクションの 1 つを選択します。
- ベクトルオプションタブで、プロット内のベクトルのサイズ、密度、および形状を定義します。
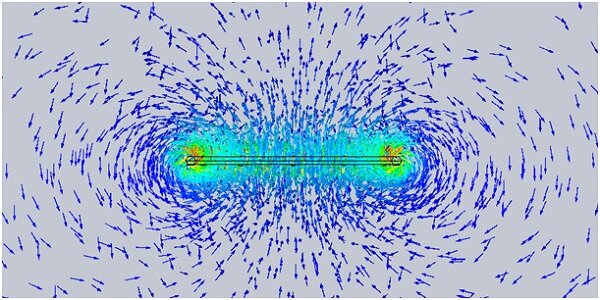
図 5 -磁束密度のセクションプロット