EMWorks Blog

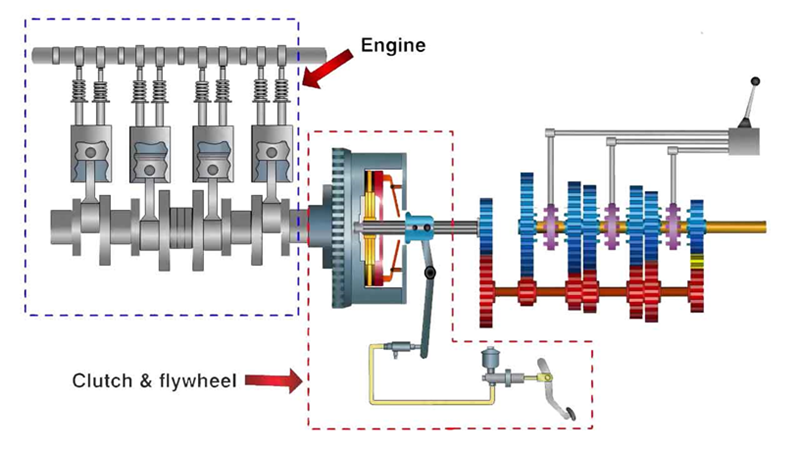
How do you design a solenoid actuator for an Automated Manual Transmission

EMWorks2D EMS - Inventor EMS - SOLIDWORKS

Learn how to design a solenoid actuator for Automated Manual Transmissions with our step-by-step guide using EMWORKS. Master the challenges of AMT actuator engineering.

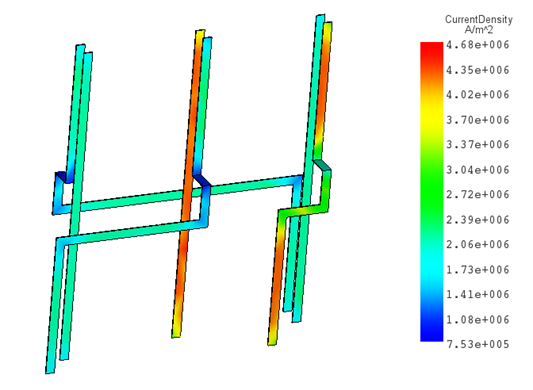
Transform your Autodesk Inventor into a High-Voltage Busbars Design Workbench

EMS - Inventor

Learn how to convert Autodesk Inventor into a high-voltage busbars design workbench with EMWORKS—optimize power systems with precision.

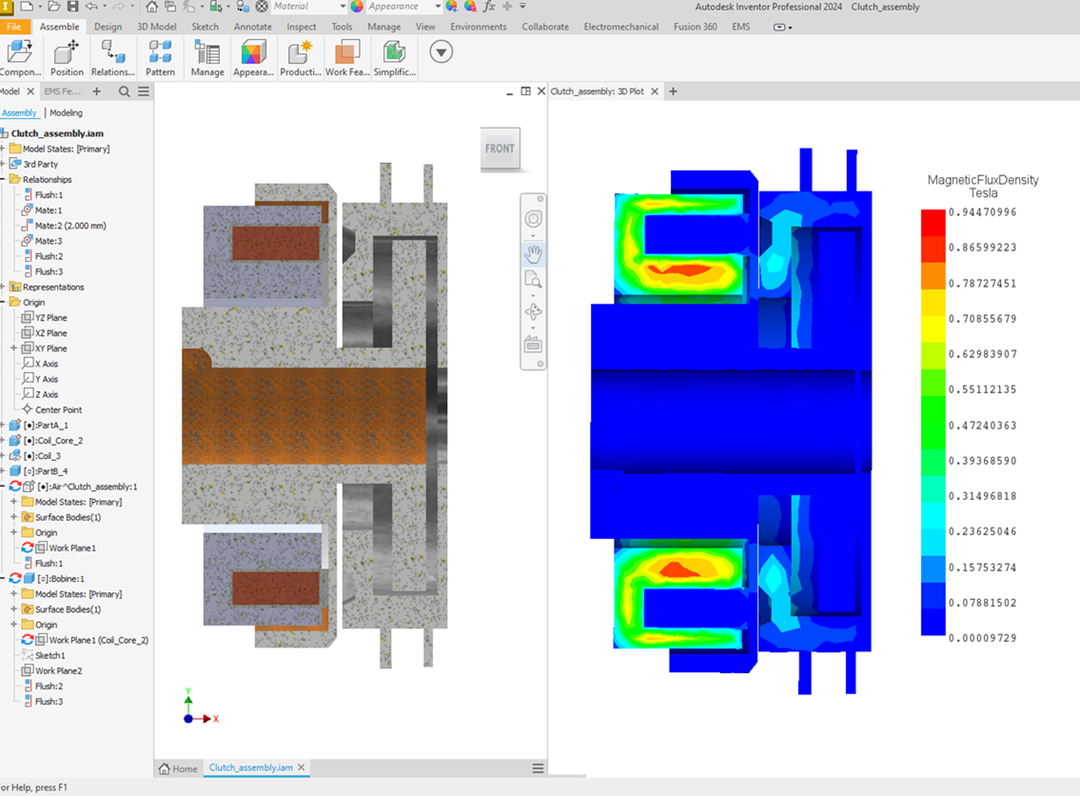
Designing A Magnetic Clutch Using Autodesk Inventor

EMS - Inventor

Discover how EMWORKS integrates with Autodesk Inventor to revolutionize magnetic clutch design, offering robust simulation tools for top performance and efficiency.

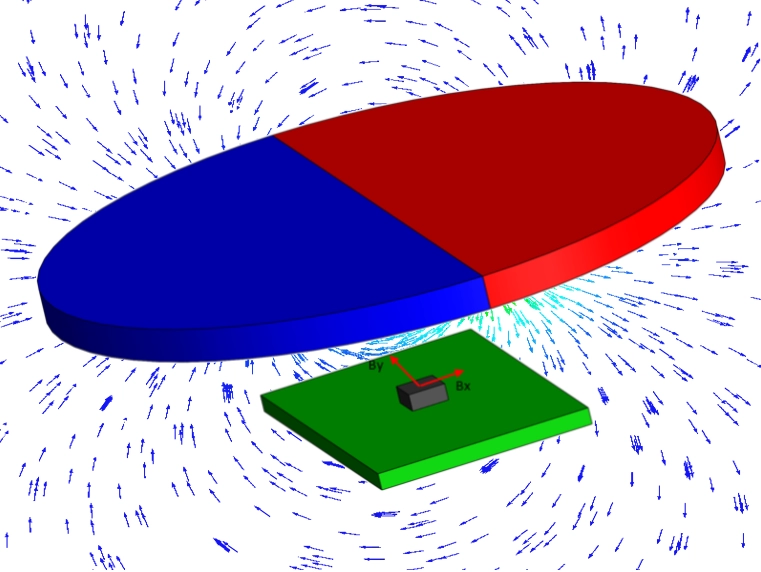
How Magnetic Encoders Enhance Precision in Motion Control and Automation

EMS

Discover how magnetic encoders operate and their pivotal role in achieving precise motion control and automation. Learn the importance of magnetization direction and Hall effect sensors.