説明
この検証例では、2 層の誘電体シリンダーにおける静電界強度の計算が考慮されています。内側の円柱の半径は a=5mm で、比誘電率は e r2=2 です。外側の円柱の半径は b =10mm で、比誘電率は e r1=5 です。システム全体は、均一な横方向の静電容量に配置されます。フィールド、E 0=E 0 x?、図 1 に示すように、公開されたデータに対して EMS の結果を検証したいと考えています [1]。
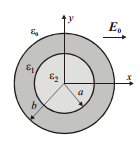
図 1: 2 層誘電体シリンダー
公開された記事では、著者は単純にそれを 2 次元構造としてモデル化しました。 EMS は、完全に 3 次元のフィールド シミュレータです。円柱はその軸に沿って均一ですが、深さが小さいことを考慮する必要があります。さらに、シリンダーの周囲の空気もモデルに含める必要があります。
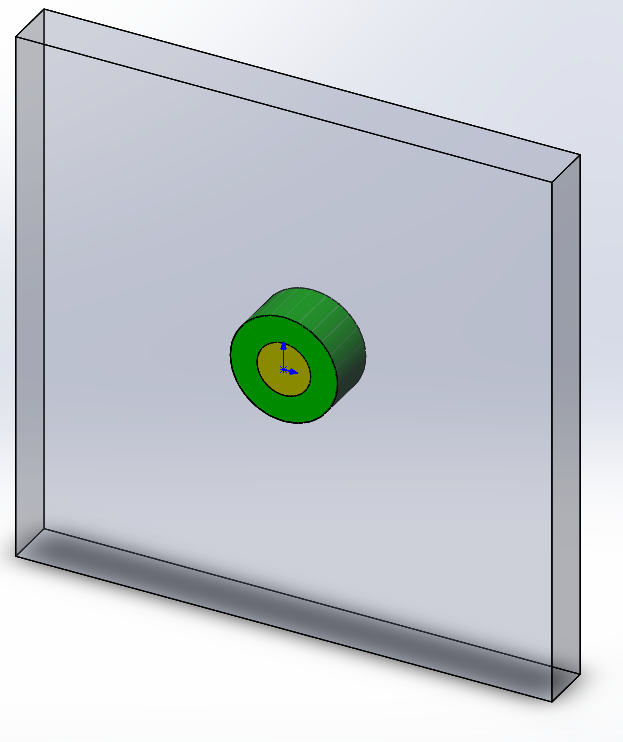
図 2:誘電体シリンダーの SolidWorks モデル
スタディ
EMS の静電モジュールは、電界強度と、誘電体シリンダーと周囲の空気領域の電位分布を計算するために使用されます。 EMS で静電スタディまたは設計シナリオを作成した後、常に 3 つの重要な手順に従う必要があります。つまり、すべてのソリッド ボディに適切な材料を適用し、必要な境界条件、または EMS のいわゆる負荷/制約を適用し、モデル全体をメッシュ化します。
材料
この例では、適用するマテリアルは 3 つだけです。表 1 にこれらの材料を示します。
コンポーネント/ボディ | 比誘電率 |
Air box | 1.0 |
Inner cylinder | 2.0 |
Outer cylinder | 5.0 |
表 1:静電スタディにおけるすべての固体の材料
材料の適用は簡単です。コンポーネント アイコンを右クリックして、マテリアルを適用するだけです。
負荷/制約
モデルの電気環境と磁気環境を定義するには、荷重と拘束が必要です。解析結果は、指定された荷重と拘束に直接依存します。荷重と拘束は、ジオメトリに完全に関連付けられ、ジオメトリの変更に合わせて自動的に調整されるフィーチャとしてジオメトリ エンティティに適用されます。
この研究で唯一適用可能な境界条件は、外部静電界です。外部静電界を模倣するために、100mm の空気領域に 10 V の電圧差が適用されます。つまり、E0=10V/0.1m=100 V/m です。
メッシング
メッシングは、設計解析において非常に重要なステップです。 EMS は、モデルの体積、表面積、およびその他の幾何学的詳細を考慮して、モデルの全体的な要素サイズを推定します。生成されるメッシュのサイズ (節点と要素の数) は、モデルのジオメトリと寸法、要素サイズ、メッシュ許容値、およびメッシュ コントロールによって異なります。おおよその結果で十分な設計解析の初期段階では、解析を高速化するために、より大きな要素サイズを指定できます。より正確な解を得るには、より小さい要素サイズが必要になる場合があります。
この特定のベンチマークでは、ジオメトリに小さな領域とギャップが伴うため、メッシングはかなり単純です。したがって、グローバル要素サイズは 10 mm に設定され、メッシュ公差は 0.01 mm です。メッシュ要素の総数を増やさずに高い精度を達成するには、大きなフィールドまたは変動が予想される領域にメッシュ コントロールを適用することをお勧めします。 1 mm のローカル メッシュ コントロールが誘電体シリンダーに適用されます。図 3 は、結果のメッシュを示しています。

図 3:構造のメッシュ
結果
実行が成功すると、静電モジュールは 3 つの結果フォルダーと結果テーブルを生成します。フォルダには、それぞれ電場E 、電気変位D 、電位分布Vが含まれています。結果テーブルには、静電蓄積エネルギーと静電容量マトリックス (該当する場合) が含まれます。さらに、すべての結果は、フリンジ、ベクトル、等高線、セクション、ライン、およびクリッピング プロットなどのさまざまな形式で視覚化できます。結果は簡単に拡大、エクスポート、分析できます。
この特定のベンチマークでは、誘電体シリンダーと周囲の空気の電界分布のフリンジ プロットが、[1] で報告されている結果と比較されます。さらに、EMS のライン プロット機能を使用して、座標 (0.0, 0.0, 0.0) と (0.75cm, 0.0, 0.0) の 2 点の電界を比較します。図 4 ~ 6 が示すように、EMS の結果は [1] の著者によって報告されたものと一致します。
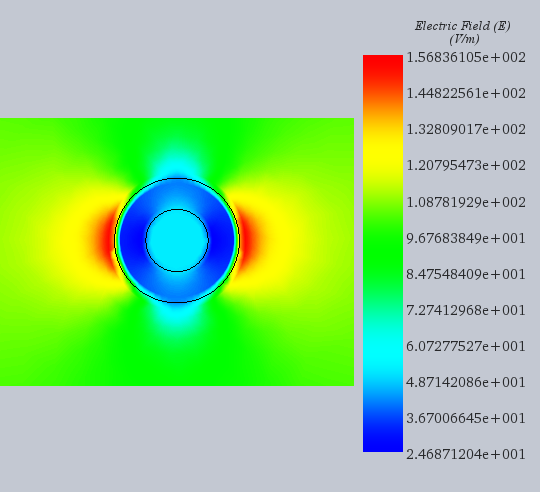
図4: EMSで得られた静電界分布
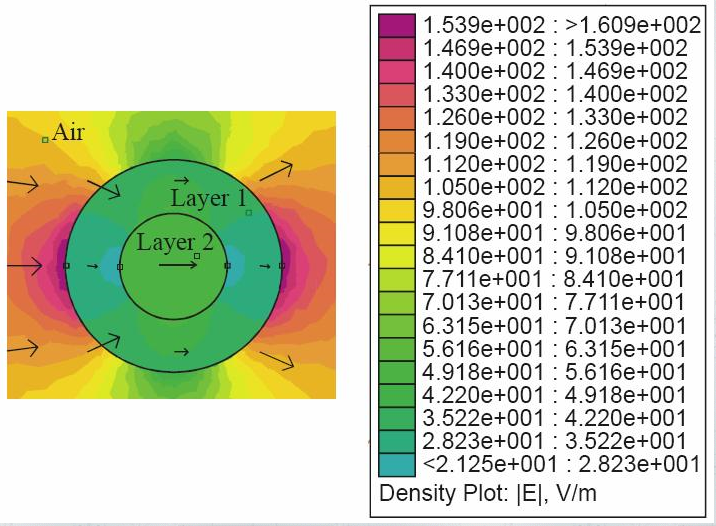
図 5: [1] で報告されている静電界分布
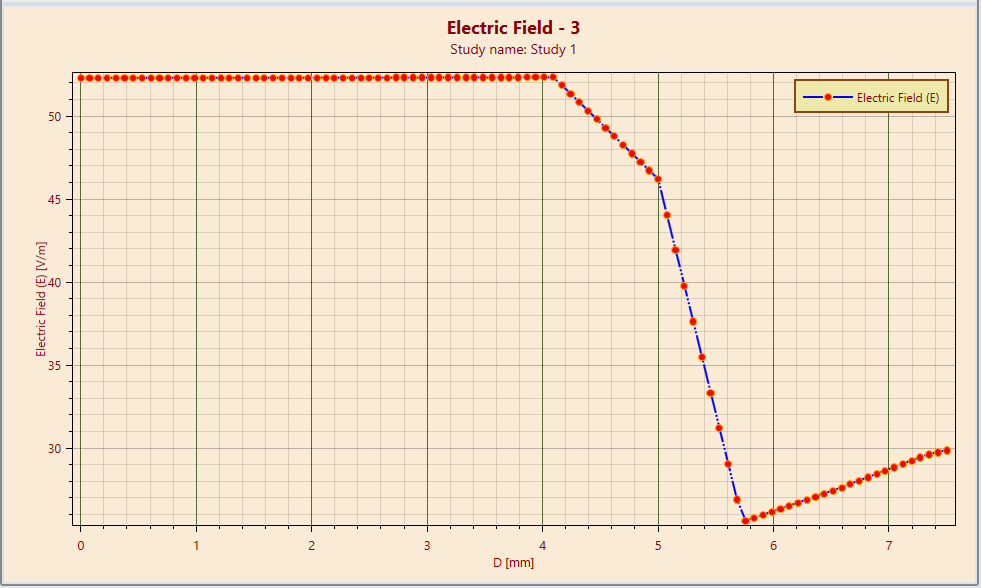
図 6: EMS によって得られた(0.0, 0.0) と (0.75cm, 0.0)の間の静電界のライン プロット
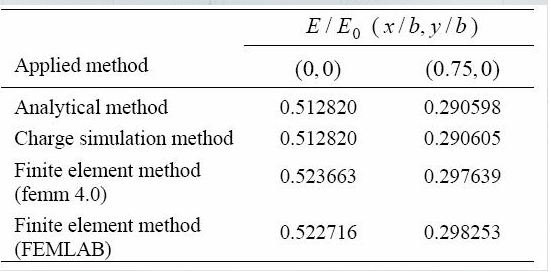
表 2: [1] で報告されている(0.0, 0.0) および (0.75cm, 0.0)での静電界